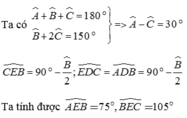Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác vuông ABE có
^ABE + ^AEB = 180 - ^BAE=180 - 90 = 90 => ^AEB < 90
Mà ^AEC=180=^AEB + ^BEC
=> ^BEC=180 - ^AEB >90 => ^BEC là góc tù

a) \(\Rightarrow\)\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\)\(\widehat{B}+\widehat{C}=180^0-90^0=90^0\)
\(\Rightarrow\)\(\widehat{EBC}< \widehat{ABC}\)
\(\Rightarrow\)\(\widehat{EBC}+\widehat{C}< 90^0\)
Mà\(\widehat{BEC}+\widehat{EBC}+\widehat{C}=180^0\)
\(\Rightarrow\)\(\widehat{EBC}+\widehat{C}< 90^0\)
\(\Rightarrow\)\(\widehat{BEC}>90^0\)(góc tù)
b)\(\Rightarrow\)\(\widehat{C}\)=\(\left(90^0+10^0\right):2=50^0\)
\(\widehat{B}=\left(90^0-10^0\right)=40^0\)
Vì\(\widehat{EBA}=\widehat{EBC}=\frac{\widehat{ABC}}{2}=\frac{40^0}{2}=20^0\)
\(\Rightarrow\)\(\widehat{A}+\widehat{EBA}+\widehat{AEB}=180^0\)
\(\widehat{AEB}=180^0-\left(90^0+20^0\right)=70^0\)
\(\Rightarrow\)\(\widehat{C}+\widehat{CEB}+\widehat{EBC}=180^0\)
\(\widehat{BEC}=180^0-\left(50^0+20^0\right)=110^0\).
(Tổng 3 góc của 1 tam giác = 1800 nha).
a)Xét tam giác vg ABD và tam giác vg IBD có
B1=B2 ( Vì BD là tia phân gíc của B )
BD chung
-> tam giác ABD= IBD
b) Vì tam giác ABD= IBD
-> DA = DI
Xét tam giác vg IDC và tam gíc vg ADE có( A = I =90 độ )
DA = DI (cmt)
D1 D2 ( đối đỉnh)
->tam giác IDC = tam gíc ADE (c-g-c)
-> DC=DE
Xét tam giác DIC vuông tại i có
DC>DI (ch>cgv)
mà DI = DE (cmt)
-> DE>DI
c) Vì tam giác ABD= IBD
-> AB = IB ( cặp cạnh tương ứng )
Tam giác IDC = tam gíc ADE
-> AE = IC (cặp cạnh tương ứng )
Lại có: AB + AE = BE
BI + IC = BC
Mà AB = IB (cmt)
AE = IC (cmt)
-> BE = BC
Xét tam gíc BEC có
BE = BC (cmt)
-> tam gíc BEC là tam giác cân tại B (đn tam gíc cân )
c) Xét tam gíc BEC có
BD là tia phân giác của B
Trong tam giác cân đừong phân giác cũng chính là đường cao
-> BD vuông góc với EC

a: Xet ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
góc ABD=góc MBD
=>ΔBAD=ΔBMD
=>BA=BM
Xét ΔBME vuông tại M và ΔBAC vuông tại A có
BM=BA
góc MBE chung
=>ΔBME=ΔBAC
=>BE=BC
=>ΔBEC cân tại B
b: Xét ΔDAE vuông tại A và ΔDMC vuông tại M co
DA=DM
góc ADE=góc MDC
=>ΔDAE=ΔDMC
=>DE=DC
=>D nằm trên trung trực của EC
mà BK là trung trực của EC
nên B,D,K thẳng hàng

A B C D E --
a) Xét hai tg AEB và AEC có
AE cạnh chungg
BAD = CAD [ Tia phân giác của góc A ]
AB = AC [ gt ]
=> tg AEB= AEC [ c - g c ]
b ) Tam giác ABC cân có AD là phân giác nên đồng thời là đường cao => AD vuông góc với BC
tg AEB = tg AEC [ cmt ]
=> EB= EC => tg BEC cân tại B , có AD là đường cao nên đồng thời là phân giác => ED là phan giác góc BEC