Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(M=\frac{2.2^{12}.3^6+2^2.2^9.3^9}{2^5.2^7.3^7+2^7.2^3.3^{10}}\)
\(=\frac{2^{11}.3^6\left(2^2+3^3\right)}{2^{10}.3^7\left(2^2+3^3\right)}\)
\(=\frac{2}{3}\)
\(M=\frac{2.\left(2^3\right)^4.\left(3^3\right)^2+2^2.\left(2.3\right)^9}{2^5.\left(2.3\right)^7+2^7.2^3.\left(3^2\right)^5}\)
\(M=\frac{2.2^{12}.3^6+2^2.2^9.3^9}{2^5.2^7.3^7+2^7.2^3.3^{10}}\)
\(M=\frac{2^{13}.3^6+2^{11}.3^9}{2^{12}.3^7+2^{10}.3^{10}}\)
\(M=\frac{2^{11}.3^6\left(2^2.1+1.3^3\right)}{2^{10}.3^7\left(2^2.1+1.3^3\right)}\)
\(M=\frac{2.31}{3.31}\)
\(M=\frac{2}{3}\)
Study well

Xét tứ giác AFBC có
N là trung điểm của AB
N là trung điểm của CF
Do đó: AFBC là hình bình hành
Suy ra: AF//BC và AF=BC
Xét tứ giác ADCB có
M là trung điểm của AC
M là trung điểm của DB
DO đó: ADCB là hình bình hành
Suy ra: AD//CB và AD=CB
Ta có: AF//BC
AD//BC
mà AD,AF có điểm chung là A
nên D,A,F thẳng hàng
mà AD=AF(=BC)
nên A là trung điểm của DF

xét ∆AMB và ∆AMC có : AM chung
AB = AC (gt)
BM = CM do M là trung điểm của BC (Gt)
=> ∆AMB = ∆AMC (c-c-c)
b, ∆AMB = ∆AMC (câu a)
=> ^AMB = ^AMC (định nghĩa)
có ^AMB + ^AMC = 180 (kề bù)
=> ^AMB = 90
=> AM _|_ BC (định nghĩa)
c, CD _|_ BC (gt)
AM _|_ BC (gt)
CD không trùng AM
=> CD // AM
Cậu tự vẽ hình nha !
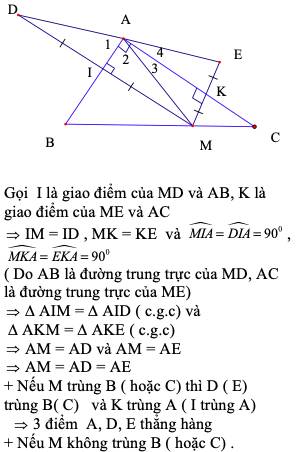
a) Vì AB là đường trung trực của DM
=> AD = AM (tính chất 1 điểm trên đường trung trực) (1)
Tương tự với AC là trung trực của ME
=> AM = AE (2)
Từ (1) và (2)
=> AM = AD = AE
b) Từ (1) ta suy ra \(\Delta ADM\) cân tại A
Từ (2) ta cũng có \(\Delta AEM\) cân tại A
Vì trong tam giác cân , đường trung trực , phân giác , trung tuyến , đường cao đều trung nhau
=> Với AB,AC là đường trung trực tương ứng thì AB,AC cũng là phân giác tương ứng
=> \(\widehat{DAB}=\widehat{MAB}=\frac{\widehat{MAD}}{2}\) và \(\widehat{MAC}=\widehat{CAE}=\frac{\widehat{MAE}}{2}\)
Ta có :
\(\widehat{BAM}+\widehat{MAC}=90^0\)
\(2\widehat{BAM}+2\widehat{MAC}=180^0\)
\(\widehat{MAD}+\widehat{MAE}=180^0\)
=> Ba điểm thẳng hàng
éo giúp