Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hinh tu ve
cm: aehf la hinh chu nhat vi co 4 goc vuong
suy ra af=eh
\(\Delta BEHdd\Delta BAC\)
\(\frac{EH}{AC}=\frac{BH}{AB}< =>\frac{EH}{BH}=\frac{AC}{AB}\)
tg_bac dd tg_ahc
\(\frac{AC}{AB}=\frac{CH}{AC}\)
suy ra
\(\frac{AF}{BH}=\frac{CH}{AC}\)(do af=eh)
\(\frac{AF}{CH}=\frac{BH}{AC}\)
a. Qua C dung duong thang vuong AC tai C cat NH tai I. De thay tg vuong CAM = tg vuong ICN (AM=CN;goc ACM=goc CIN) =>IC=CA => ACIB la hinh vuong Goi J la trung diem IC. BJ giao NI tai ok De thay BJ // CM => ok la trung diem IH va BK vuong goc IN (Do CM vuong goc IN tai H) => BK vua la duong cao, vua la trung tuyen cua tg BHI =>tg BHIcan tai B =>BH=BI ma ACIB la hinh vuong => BH=BI=BA => ABH can tai B b. De thay tu giac MBIH noi tiep (B=H=ninety) =>goc BIM = goc BHM (cung chan BM) (a million) Mat khac vi HE vuong goc AB => HE // AC => goc EHM = goc ACM (goc dong vi) (2) Hon nua tg AMC = tg BMI => goc BIM = goc ACM (3) Tu (a million), (2), (3) => goc BHM = goc EHM => HM la phan giac goc BHE

a, bc^2 = ab^2 +ac^2
<=.> (ae+eb)^2 +(af+fc)^2
<=.>AE^2 +2 AE.EB +EB^2 +AF^2+FC^2+2AF,FC
<=> EF^2 +EB^2 +CF^2 +2.(EH^2+FH^2)
<=>EB^2 +CF^2 + AH ^2 + 2 AH^2 vì tứ giác EHAF là hcn suy ra AH =EF
<=>EB^2 +CF^2+3 AH^2 (đpcm)
b, cb =2a là thế nào vậy

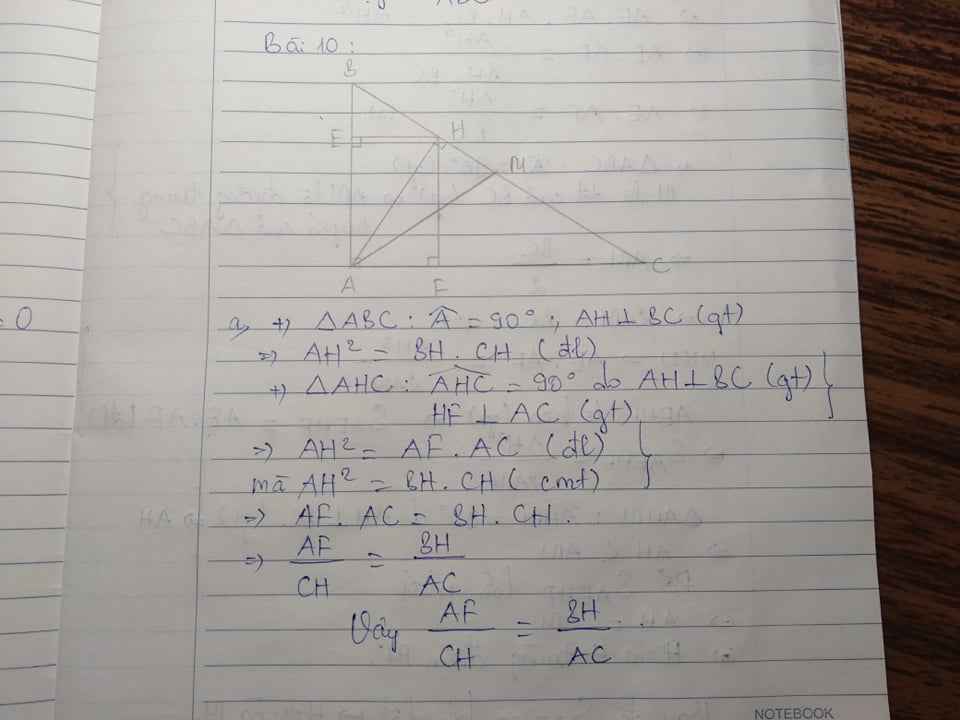
a: Xét ΔHEB vuông tại E và ΔCHA vuông tại H có
\(\widehat{EHB}=\widehat{HCA}\)
Do đó: ΔHEB\(\sim\)ΔCHA
Suy ra: \(\dfrac{HE}{CH}=\dfrac{BH}{AC}\left(1\right)\)
Xét tứ giác AEHF có
\(\widehat{AFH}=\widehat{AEH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: HE=AF(2)
từ (1) và (2) suy ra \(\dfrac{AF}{CH}=\dfrac{BH}{AC}\)