Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

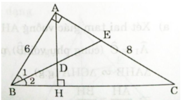
a) Ta có BE là phân giác của ∠ABC (gt)
⇒ ∠B1 = ∠B2
Do đó hai tam giác vuông:
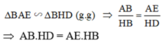
b) Ta có:
![]()
(định lý Pitago)
Xét hai tam giác vuông AHB và CAB có góc B chung nên :
![]()
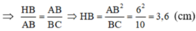
![]()


a)
Xét \(\Delta ABC\)và \(\Delta HBA\) có:
\(\widehat{A}=\widehat{H}=90^o\)
\(\widehat{B}\)là góc chung
\(\Rightarrow\Delta ABC\)đồng dạng với \(\Delta HBA\)
\(\RightarrowĐpcm\)
b)
Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat{A}=\widehat{H}=90^o\)
\(\widehat{C}\)là góc chung
\(\Rightarrow\Delta ABC\)đồng dạng với \(\Delta HAC\)
\(\Rightarrow\Delta HBA\)đồng dạng với \(\Delta HAC\) (bắc cầu)
Vì \(\Delta HBA\)đồng dạng với \(\Delta HAC\)
\(\Rightarrow\frac{AH}{HC}=\frac{HB}{AH}\Rightarrow AH^2=HB.HC\Rightarrowđpcm\)

a/ Xét tg HBA và tg ABC, có:
góc BHA = góc BAC = 90 độ
góc B chung
Suyra: tg HBA đồng dạng với tg ABC (g-g)
b/ Ta có tg ABC vuông tại A:
\(BC^2=AC^2+AB^2\)
\(BC^2=8^2+6^2=100\)
\(\Rightarrow BC=\sqrt{100}=10\)(cm)
Ta có: \(\frac{HA}{AC}=\frac{BA}{BC}\)(tg HBA đồng dạng với tg ABC)
\(\Rightarrow\frac{HA}{8}=\frac{6}{10}\)
\(\Rightarrow HA=\frac{8.6}{10}=4,8\left(cm\right)\)

A B C 6 8 H E D
a, Xét tam giác ABC và tam giác HBA ta có :
^BAC = ^AHB = 900
^B _ chung
Vậy tam giác ABC ~ tam giác HBA ( g.g )
c, tam giác ABC vuông tại A, có đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=36+64=100\Rightarrow BC=10\)cm
Ta có : \(\dfrac{AC}{AH}=\dfrac{BC}{AB}\)( cặp tỉ số đồng dạng ý a )
\(\Rightarrow\dfrac{8}{AH}=\dfrac{10}{6}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}\)cm
d, phải là cắt AC nhé, xem lại đề nhé bạn

Hình thì bạn tự vẽ nha
a)Xét tam giác ABC và tam giá HBA, có:
Góc B chung
Góc BAC = góc BHA
--> Tam giác ABC ~ Tam giác HBA
b)Xét tam giác AHB và tam giác HCA, có
Góc A - góc H
Góc ABH = Góc AHC
-->tam giác AHB ~ tam giác AHC
-->AH/HB = HC/AH
-->AH.AH = HB.HC
-->AH^2=HB.HC(đpcm)
c)
+) Áp dụng định lý PTG vào tam giác vuông ABC, có :
BC^2=AB^2 + AC^2
<--> 6^2 + 8^2 = 100
--> BC = 10(cm)
+)Vì tam giác ABC ~ Tam giác HBA :
AB/HB = BC/BA = AC/HA
-)AB/HB = BC/BA
= 6/HB =10/6
--> HB = 6.6/10
-->HB = 3,6(cm)
-)BC/BA =AC/HA
=10/6 = 8/HA
--> HA = 6.8/10
--> HA = 4,8 (cm)
d) tính tỉ số diện tích thì bạn ghi tỉ số đồng dạng ra rồi bình phương tỉ số đó lên
là đc tỉ số đồng dạng ạ
xét tam giác ABC có BC2=ab2 + ac2
thay số BC2=62+82
BC2=36+64=100
BC=10(cm)
còn lại mình không bít,xin lỗi
a: Đề sai rồi bạn
b: BC=căn 8^2+6^2=10cm
S ABC=1/2*AB*AC=24cm2
Xét ΔBAH vuông tại H và ΔBCA vuông tại A có
góc B chung
=>ΔBAH đồng dạng với ΔBCA
=>BA/BC=BH/BA=6/10=3/5 và S BAH/S BCA=(3/5)^2=9/25
=>DH/DA=3/5
=>HD/HA=3/8
=>S BHD=3/8*S HBA=3/8*9/25*S BCA=27/200*S BCA