Cho tam giác ABC vuông tại A, trung tuyến AD. I là trung điểm của AB, K là điểm dối xứng của D qua I. a. Tứ giác AKBD l...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

LP

lê phương thảo

1 tháng 1 2020

Cho tam giác ABC vuông tại A, trung tuyến AD. I là trung điểm của AB, K là điểm dối xứng của D qua I.

a. Tứ giác AKBD là hình gì

b. Chứng minh tứ giác AKBC là hình bình hành.

c. Cho AB =3cm, AC= 4cm. Tính chu vi AKDC

1

ND

Nguyễn Duy Khang

1 tháng 1 2020

https://i.imgur.com/fEDscrX.jpg

Các câu hỏi dưới đây có thể giống với câu hỏi trên

LN

lê nguyễn hà chi

12 tháng 12 2021

Tam giác ABC vuông tại A có trung tuyến là AD, E là trung điểm AB, K
đối xứng của D qua E.
a) Chứng minh K đối xứng D qua AB
b) Tứ giác AKDC, ADBK là hình gì?
c) Cho BC = 8cm. Tính chu vi tứ giác ADBK
d) Tam giác ABC cần thêm điều kiện gì để ADBK là hình vuông v

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 12 2021

b: Xét tứ giác ADBK có

E là trung điểm của AB

E là trung điểm của DK

Do đó: ADBK là hình bình hành

mà DA=DB

nên ADBK là hình thoi

TN

Trâm Ngọc

5 tháng 10 2021

Cho tam giác ABC vuông tại A có đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm đối xứng với M qua D

a) chứng minh tứ giác AEBM là hình thoi

b) cho AB=3cm, AC=4cm. Tính chu vi hình thoi AEBM

c) tứ giác AEMC là hình gì? Vì sao?

d) Gọi I là trung điểm của AM. Chứng minh E,I,C thẳng hàng

1

NL

Nguyễn Lê Phước Thịnh

5 tháng 10 2021

a: Ta có: ΔABC vuông tại A

mà AM là đường trung tuyến ứng với cạnh huyền BC

nên AM=BM=CM=BC/2

Xét tứ giác AMBE có

D là trung điểm của đường chéo AB

D là trung điểm của đường chéo ME

Do đó: AMBE là hình bình hành

mà AM=BM

nên AMBE là hình thoi

TT

Trần Thị Tú Oanh

26 tháng 11 2021

Cho tam giác ABC vuông tại A (AB<AC) . Đường trung tuyến AM . Gọi I là trung điểm của AB và D là điểm đối xứng với M qua I a, Tính diện tích tam giác ABC biết AB=3cm, AC= 4cm b, Chứng minh tứ giác DAMB là hình thoi c, Chứng minh tứ giác DACM là hình bình hành d, Tìm điều kiện của tam giác ABC để tứ giác ADBM là hình...

0

QC

Quynh Chi

21 tháng 9 2021

Bài 6: Cho tam giác ABC vuông tại A có trung tuyến là AD, E là trung điểm AB, K là điểm đối xứng của D qua E. a) Chứng minh K đối xứng với D qua AB b) Tứ giác AKDC, ADBK là hình gì? c) Tam giác ABC cần có thêm điều kiện gì để ADBK là hình vuông? d) Đường thẳng qua D vuông góc với AC cắt đường thẳng AK tại I. Tính diện tích của tứ giác BDIK theo diện tích của tam giác ABC.

1

NL

Nguyễn Lê Phước Thịnh

21 tháng 9 2021

a: Ta có: ΔABC cân tại A

mà AD là đường trung tuyến ứng với cạnh huyền BC

nên \(AD=BD=CD=\dfrac{BC}{2}\)

Xét tứ giác ADBK có

E là trung điểm của đường chéo AB

E là trung điểm của đường chéo DK

Do đó: ADBK là hình bình hành

mà DA=DB

nên ADBK là hình thoi

Suy ra: K đối xứng với D qua AB

b: Xét ΔABC có

E là trung điểm của AB

D là trung điểm của BC

Do đó: DE là đường trung bình của ΔABC

Suy ra: DE//AC và \(DE=\dfrac{AC}{2}\)

mà \(DE=\dfrac{DK}{2}\)

nên DK//AC và DK=AC

hay AKDC là hình bình hành

NH

Nguyễn Huyền Anh

31 tháng 10 2018 - olm

Cho tam giác ABC vuông tạo A, BC= 4cm, trung tuyến AM, K là trung diểm AC,N là điểm đối xứng với M qua K. Chứng minh:

a) Tứ giác ANCM là hình thoi? Tính chu vi

b) Tứ giác ANMB là hình bình hành

c) Tam giác ABC cần thêm điều kiện gì ANCM là hình vuông

d) H là trung điểm của am, KH cắt AB tại . Chứng minh MI vông góc với AB

1

AH

AE Hợp Lực

31 tháng 10 2018

Đây không phải câu hỏi linh tinh nha các bạn:

Thay mặt người phân phối chương trình xin tặng chương trình học online số 1 Việt Nam. Sự kiện bắt đầu từ ngày 28/10 đến 1/11

Xin chào các thành viên đang online trên trang. Sự kiện khuyến mãi được tài trợ 500 suất áo chiếc áo đá bóng Việt Nam.Mong tất cả mọi người đã xem vào truy cập sau để nhận thưởng khi xem có 1 bản đăng kí nhận miễn phí : Thời gian có hạn tặng mọi người đã tham gia tích cực -> Không tin các bạn có thể hỏi các CTV nha mình chỉ có quyền thông báo :

Copy cái này hoặc gõ :

https://lazi.vn/quiz/d/16491/nhac-edm-la-loai-nhac-the-loai-gi

mn

PT

Pham Trong Bach

31 tháng 8 2019

Cho tam giác ABC vuông tại A, đường trung tuyến AM. Gọi D là trung điểm của AB, E là điểm dối xứng với M qua D.

a) Chứng minh rằng điểm E đối xứng với điểm M qua AB.

b) Các tứ giác AEMC, AEBM là hình gì? Vì sao?

c) Cho BC = 4cm, tính chu vì tứ giác AEBM.

d) Tam giác vuông ABC có điều kiện gì thì AEBM là hình vuông?

1

CM

Cao Minh Tâm

31 tháng 8 2019

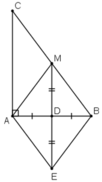
Giải bài 89 trang 111 Toán 8 Tập 1 | Giải bài tập Toán 8

a) Ta có MB = MC, DB = DA

⇒ MD là đường trung bình của ΔABC

⇒ MD // AC

Mà AC ⊥ AB

⇒ MD ⊥ AB.

Mà D là trung điểm ME

⇒ AB là đường trung trực của ME

⇒ E đối xứng với M qua AB.

b) + MD là đường trung bình của ΔABC

⇒ AC = 2MD.

E đối xứng với M qua D

⇒ D là trung điểm EM

⇒ EM = 2.MD

⇒ AC = EM.

Lại có AC // EM

⇒ Tứ giác AEMC là hình bình hành.

+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.

Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.

c) Ta có: BC = 4cm ⇒ BM = 2cm

Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm

d)- Cách 1:

Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC

Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.

- Cách 2:

Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM

⇔ ΔABC có trung tuyến AM là đường cao

⇔ ΔABC cân tại A.

Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.

S

smile

27 tháng 8

tại sao AC //EM vậy ạ ?

2N

21_thuy nhã _8a3

4 tháng 12 2021

Cho hình tam giác ABC vuông tại A , đường trung tuyến AD . Gọi I là trung điểm của AC và E là điểm đối xứng với D qua E.

a) Chứng minh tứ giác ADCE là hình thoi

Cho AB = 3cm ; AC = 4cm . Tính độ dài cạnh hình thoi ADCE

3

2N

21_thuy nhã _8a3

4 tháng 12 2021

mình cần gấp á

NL

Nguyễn Lê Phước Thịnh

4 tháng 12 2021

a: Xét tứ giác ADCE có

I là trung điểm của AC

I là trung điểm của DE

Do đó: ADCE là hình bình hành

mà AD=CD

nên ADCE là hình thoi

AC

Ari chan

26 tháng 1 2022

Cho tam giác ABC vuông tại A, trung tuyến AM. Gọi I là trung điểm của AB, N là điểm đối xứng với M qua I. a) C/m tứ giác ANMC là hình bình hành b) c/m tứ giác AMBN là hình thoi c) Cho AB 4cm; AC = 6cm. Tính diện tích tứ giác AMBN d) Tam giác vuông ABC có điều kiện gì thì tứ giác AMBN là hình vuông...

1

TH

Thanh Hoàng Thanh

26 tháng 1 2022

a) AM là trung tuyến (gt). => M là trung điểm của BC.

=> BM = MC = \(\dfrac{1}{2}\) BC.

Xét tứ giác AMBN:

I là trung điểm của AB (gt).

I là trung điểm của NM (N là điểm đối xứng với M qua I).

=> Tứ giác AMBN là hình bình hành (dhnb).

=> AN = BM và AN // BM (Tính chất hình bình hành).

Mà BM = MC (cmt).

=> AN = MC.

Xét tứ giác ANMC:

AN = MC (cmt).

AN // MC (AN // BM).

=> Tứ giác ANMC là hình bình hành (dhnb).

b) Xét tam giác ABC vuông tại A:

AM là trung tuyến (gt).

=> AM = \(\dfrac{1}{2}\) BC (Tính chất đường trung tuyến trong tam giác vuông).

Mà BM = MC = \(\dfrac{1}{2}\) BC (cmt).

=> AM = BM = MC = \(\dfrac{1}{2}\) BC.

Xét hình bình hành AMBN: AM = BM (cmt).

=> Tứ giác AMBN là hình thoi (dhnb).

c) Tứ giác ANMC là hình bình hành (cmt).

=> NM = AC (Tính chất hình bình hành).

Mà AC = 6 cm (gt).

=> NM = AC = 6 cm.

\(S_{AMBN}=\dfrac{1}{2}.AB.NM=\dfrac{1}{2}.4.6=12\left(cm^2\right).\)

d) Tứ giác AMBN là hình vuông (gt).

=> \(\widehat{AMB}=90^o\) (Tính chất hình vuông).

=> \(AM\perp BC.\)

Xét tam giác ABC vuông tại A:

AM là trung tuyến (gt).

AM là đường cao \(\left(AM\perp BC\right).\)

=> Tam giác vuông ABC vuông cân tại A.

CN

chủ nick đg bận :)))

8 tháng 1 2022

Cho tam giác ABC vuông tại A , đường trung tuyến AM , có AB= 3cm , AC=4cm . Gọi D là trung điểm của AB,E là điểm đối xứng với M qua D .1) Tính các độ dài BC,DM.2) Chứng minh tứ giác AEMC là hình bình hành và tứ giác AEBM là hình thoi.3) Đường thẳng CE cắt AB tại N . Tính độ dài...

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 1 2022

1: BC=5cm

Xét ΔABC có

D là trung điểm của AB

M là trung điểm của BC

Do đó: DM là đường trung bình

=>DM=AC/2=2(cm)

2: Xét tứ giác ACME có

ME//AC

ME=AC

Do đó: ACME là hình bình hành

Xét tứ giác AEBM có

D là trung điểm của ME

D là trung điểm của AB

Do đó: AEBM là hình bình hành

mà MA=MB

nên AEBM là hình thoi