Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B E C A D F
Xét \(\Delta ABD\) và \(\Delta EBD\)
ta có DA = DE ( gt )
BA = BE ( gt )
BD là cạnh chung
=> \(\Delta ABD=\Delta EBD\left(c.c.c\right)\)

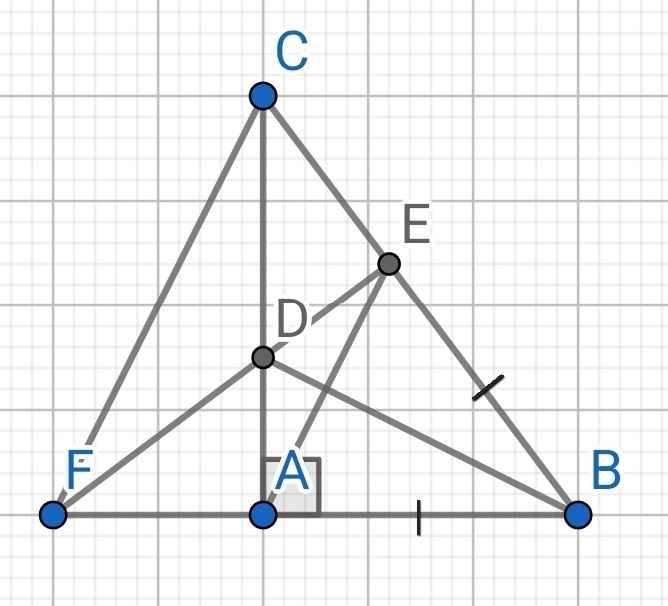 a) Xét ∆ABD và ∆EBD có:
a) Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (BD là tia phân giác của ABC)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
b) Do ∆ABD = ∆EBD (cmt)
⇒ AD = ED (hai cạnh tương ứng)
Lại do ∆ABD = ∆EBD (cmt)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ ∠DAF = ∠DEC = 90⁰
Xét hai tam giác vuông: ∆DAF và ∆DEC có:
AD = ED (cmt)
∠ADF = ∠EDC (đối đỉnh)
⇒ ∆DAF = ∆DEC (cạnh góc vuông - góc nhọn kề)
⇒ AF = EC (hai cạnh tương ứng)
c) ∆BAE có:
AB = BE (gt)
⇒ ∆BAE cân tại B
⇒ ∠BEA = ∠BAE = (180⁰ - ∠ABC) : 2 (1)
Do AF = EC (cmt)
AB = BE (gt)
⇒ AF + AB = EC + BE
⇒ BF = BC
⇒ ∆BFC cân tại B
⇒ ∠BCF = ∠BFC = (180⁰ - ∠ABC) : 2 (2)
Từ (1) và (2) suy ra:
∠BEA = ∠BCF
Mà ∠BEA và ∠BCF là hai góc đồng vị
⇒ AE // CF

a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
SUy ra: AF=EC và DF=DC (1)
c: Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE
và AF=EC
nên BF=BC(2)
Từ (1) và (2) suy ra BD⊥CF

b) Lấy điểm I thuộc cạnh AB sao cho IA = AN
Chứng minh \(\Delta\)MAN = \(\Delta\)MAI => MN = MI(1)
và ^MIA = ^MNA => ^MIB = ^MNC mà ^MNC = ^MBA => ^MIB = ^MBA hay ^MIB = ^MBI
=> \(\Delta\)MBI cân => MB = MI (2)
Từ (1) ; (2) => MN = MB

Tham khảo
Câu hỏi của Hot girl 2k5 - Toán lớp 7 - Học toán với OnlineMath
mik ko hieu cau c cho lam, ai giang giup mik cau c voi :((

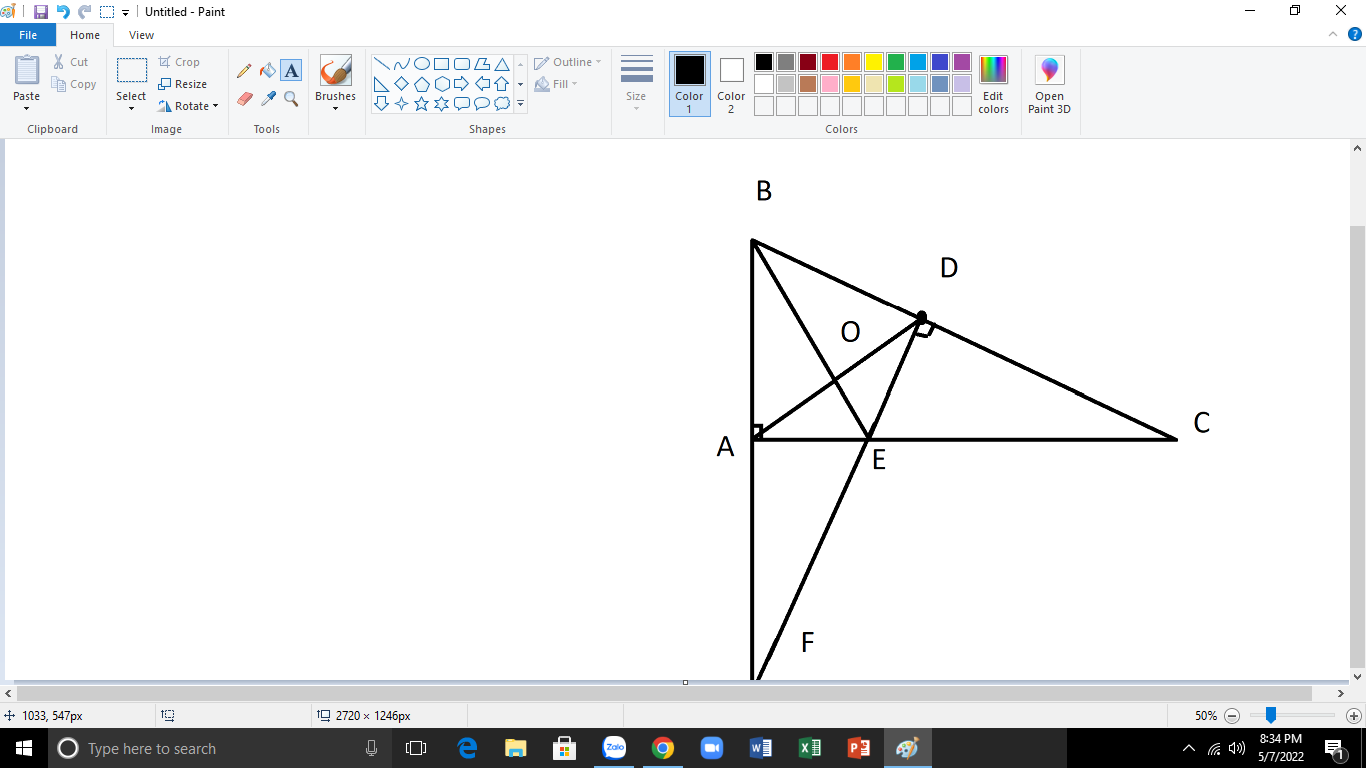
\(\text{a)Xét }\Delta ABC\text{ vuông tại A có:}\)
\(BC^2=AB+AC^2\left(\text{định lí Py ta go}\right)\)
\(\Rightarrow BC^2=5^2+7^2=25+49=74\left(cm\right)\)
\(\Rightarrow BC=\sqrt{74}\left(cm\right)\)
\(\text{b)Xét }\Delta ABE\text{ và }\Delta DBE\text{ có:}\)
\(\widehat{BAE}=\widehat{BDE}=90^0\left(gt\right)\)
\(BE\text{ chung}\)
\(BA=BD\left(gt\right)\)
\(\Rightarrow\Delta ABE=\Delta DBE\left(c-g-c\right)\)
\(\text{c)Xét }\Delta AEF\text{ và }\Delta DEC\text{ có:}\)
\(\widehat{AEF}=\widehat{DEC}\left(\text{đối đỉnh}\right)\)
\(\widehat{FAE}=\widehat{CDE}=90^0\left(gt\right)\)
\(AE=DE\left(\Delta ABE=\Delta DBE\right)\)
\(\Rightarrow\Delta AEF=\Delta DEC\left(g-c-g\right)\)
\(\Rightarrow EF=EC\left(\text{hai cạnh tương ứng}\right)\)
\(\text{d)Gọi O là giao điểm của BE và AD}\)
\(\text{Xét }\Delta ABO\text{ và }\Delta DBO\text{ có:}\)
\(BO\text{ chung}\)
\(BA=BD\left(gt\right)\)
\(\widehat{ABO}=\widehat{DBO}\left(\Delta ABE=\Delta DBE\right)\)
\(\Rightarrow\Delta ABO=\Delta DBO\left(c-g-c\right)\)
\(\Rightarrow\widehat{AOB}=\widehat{DOB}\left(\text{hai góc tương ứng}\right)\)
\(\text{Mà chúng kề bù}\)
\(\Rightarrow\widehat{AOB}=\widehat{DOB}=\dfrac{180^0}{2}=90^0\)
\(\Rightarrow BE\perp AD\)
\(\text{Mà AO=DO}\left(\Delta AOB=\Delta DOB\right)\)
\(\Rightarrow BE\text{ là đường trung trực của đoạn thẳng AD}\)
cảm ơn bạn nghe thank you mà làm thế này đúng ko bạn:
a) Vì tam giác BAC vuông tại A
=> AB^2 + AC^2 = BC^2 ( đl pytago )
=> BC^2 = 5^2 + 7^2 = 74
=> BC = căn bậc 2 của 74
b)
Xét tam giác ABE; tam giác DBE có :
AB = DB ( gt)
góc ABE = góc DBE ( gt)
BE chung
=> tam giác ABE = tam giác DBE (c.g.c) - đpcm
c)
Vì tam giác ABE = tam giác DBE (câu b)
=> AE = DE
Xét tg AEF ⊥ tại A; tg DEC ⊥ tại D:
AE = DE (c/m trên)
g AEF = g DEC (đối đỉnh)
=> tg AEF = tg DEC (cgv - gn) - đpcm
=> EF = EC
d)
Do tam giác AEF = tam giác DEC (câu c)
=> AE = DE
=> E ∈ đường trung trực của AD (1)
Lại do AB = BD (gt)
=> B ∈ đường trung trực của AD (2)
Từ (1) và (2) => BE là đường trung trực của AD. - đpcm


Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
\(\widehat{EBF}\) chung
Do đó: ΔBEF=ΔBAC
=>BF=BC
Ta có: BF=BA+AF
BC=BE+EC
mà BF=BC và BA=BE
nên AF=EC