Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
=>D nằm trên đường trung trực của AE(1)
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(2)
Từ (1) và (2) suy ra BD là đường trung trực của AE
b: Sửa đề: AF=EC
Ta có: ΔBAD=ΔBED
=>\(\widehat{BAD}=\widehat{BED}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BED}=90^0\)
=>DE\(\perp\)BC
Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó;ΔDAF=ΔDEC
=>AF=EC
c: Sửa đề: CM AE//CF
Xét ΔBFC có \(\dfrac{BA}{AF}=\dfrac{BE}{EC}\)
nên AE//CF
d: Sửa đề: I là trung điểm của FC
Ta có: IF=IC
=>I nằm trên đường trung trực của CF(3)
Ta có: DF=DC(ΔDAF=ΔDEC)
=>D nằm trên đường trung trực của CF(4)
ta có: BA+AF=BF
BE+EC=BC
mà BA=BE
và AF=EC
nên BF=BC
=>B nằm trên đường trung trực của CF(5)
Từ (3),(4),(5) suy ra B,D,I thẳng hàng

A B C E F D
a, Số đo góc ABC la :
goc A+goc B+goc C=180
130+C=180
C=50
=> số đo góc ABD là : goc ABD=1/2gocC=>25
b, Xet 2 tam giac ABD va BDE
Co:AB=BE
goc ABD=goc DBE (250)
BD canh chung =>dpcm
mình biết làm mấy câu đầu rồi, mình chỉ bí câu cuối thôi
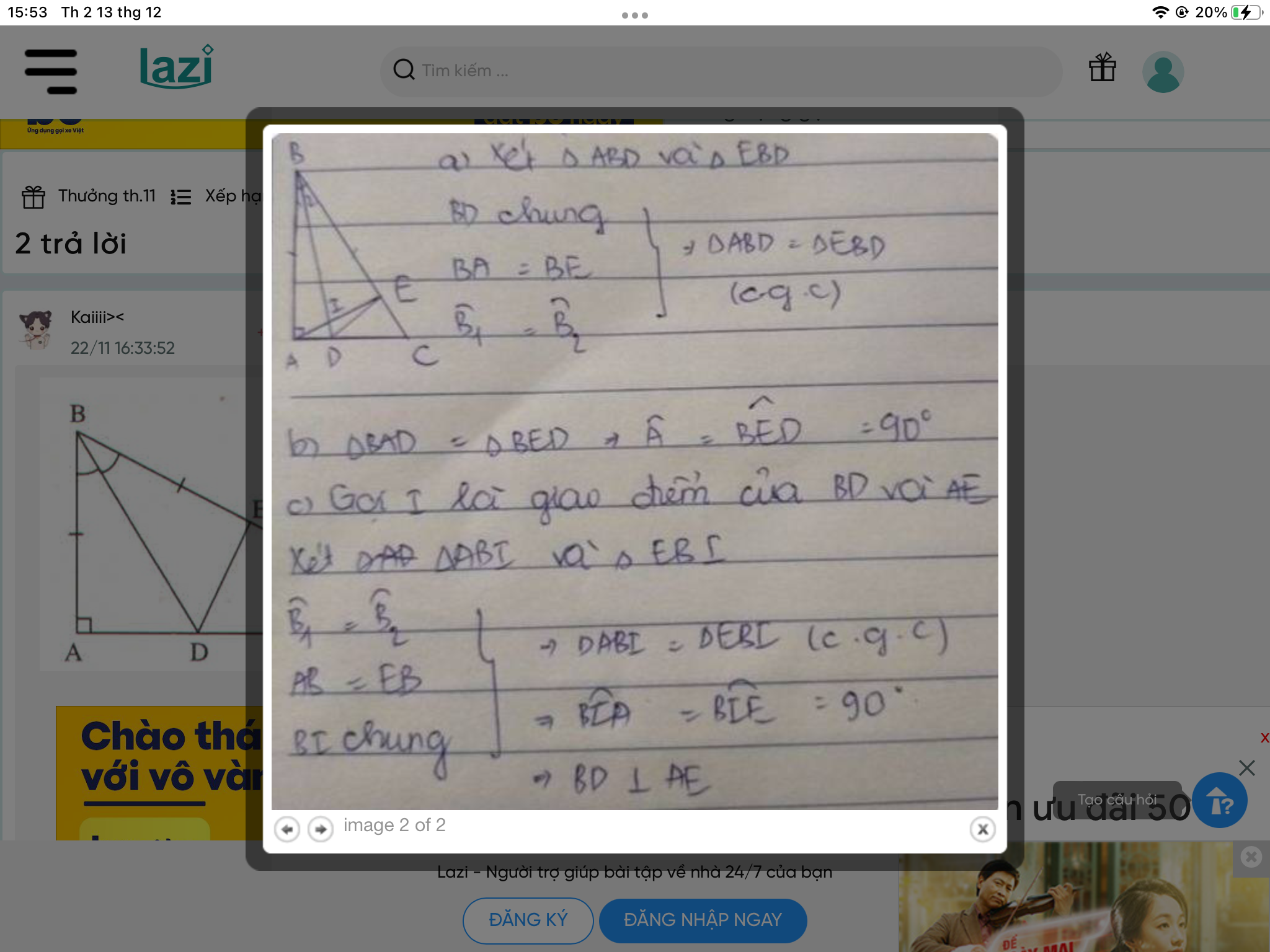
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
DO đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
nên DA=DE và \(\widehat{BAD}=\widehat{BED}=90^0\)
c: Ta có: ΔBAE cân tại B
mà BI là đường phân giác
nên BI vừa là đường cao vừa là đường trung tuyến
=>I là trung điểm của AE và BD\(\perp\)AE
=>AI=EI