Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAE vuông tại A và ΔBKE vuông tại K có
BE chung
góc ABE=góc KBE
=>ΔBAE=ΔBKE
b: Xét ΔEAM vuông tại A và ΔEKC vuông tại K có
EA=EK
góc AEM=góc KEC
=>ΔEAM=ΔEKC
=>EM=EC và AM=KC
c: Xét ΔBMC có BA/AM=BK/KC
nên AK//MC
d: BM=BC
Em=EC
=>BE là trung trực của MC
=>B,E,N thẳng hàng

a: Xét ΔABE vuông tại A và ΔKBE vuông tại K có
BE chung
\(\widehat{ABE}=\widehat{KBE}\)
Do đó: ΔABE=ΔKBE
b: Xét ΔAEM vuông tại A và ΔKEC vuông tại K cso
EA=EK
\(\widehat{AEM}=\widehat{KEC}\)
Do đó:ΔAEM=ΔKEC
Suy ra: EM=EC
c: Xét ΔBMC có BA/AM=BK/KC
nên AK//MC

a: Xét ΔABE vuông tại A và ΔKBE vuông tại K có
BE chung
\(\widehat{ABE}=\widehat{KBE}\)
Do đó: ΔABE=ΔKBE
b: Xét ΔAEM vuông tại A và ΔKEC vuông tại K có
EA=EK
\(\widehat{AEM}=\widehat{KEC}\)
Do đó: ΔAEM=ΔKEC
Suy ra: EM=EC
c: Xét ΔBMC có BA/AM=BK/KC
nên AK//MC

a: Xét ΔBAE vuông tại A và ΔBKE vuông tại K có
BE chung
\(\widehat{ABE}=\widehat{KBE}\)
Do đó: ΔBAE=ΔBKE
b: ta có: ΔBAE=ΔBKE
=>EA=EK
Xét ΔEAM vuông tại A và ΔEKC vuông tại K có
EA=EK
\(\widehat{AEM}=\widehat{KEC}\)(hai góc đối đỉnh)
Do đó: ΔEAM=ΔEKC
=>EM=EC
c: Ta có: ΔEAM=ΔEKC
=>AM=KC
Ta có: ΔBAE=ΔBKE
=>BA=BK
Xét ΔBMC có \(\dfrac{BA}{AM}=\dfrac{BK}{KC}\)
nên AK//MC
d: Ta có: NM=NC
=>N nằm trên đường trung trực của MC(1)
Ta có: EM=EC
=>E nằm trên đường trung trực của CM(2)
Ta có: BA+AM=BM
BK+KC=BC
mà BA=BK và AM=KC
nên BM=BC
=>B nằm trên đường trung trực của MC(3)
Từ (1),(2),(3) suy ra B,E,N thẳng hàng

Xét tam giác ABE vuông tại A và tam giác HBE vuông tại H ta có
BE = BE ( cạnh chung ) ; góc ABE = góc HBE ( BE là tia phân giác góc B )
--> tam giác ABE = tam giác HBE ( ch = gn )
b ) ta có :
BA = BH ( tm giác ABE = tam giác HBE )
EA = EH ( tam giác ABE = tam giác HBE )
==> BE là đường trung của của AH
Xét tam giác EKA và tam giác ECH ta có :
AE = EH ( tam giác ABE = tam giác HBE ) ; góc EAK = góc EHC ( =90 ) góc AEK = góc HEC
-->tam giác EAK = tam giác ECH ( g--c--h )
--> EK =EC ( 2 cạnh tương ứng )
d) từ điểm E đến đường thẳng HC tacó :
EH là đường vuông góc ( EH vuông góc BC )
EC là đường xuyên
-> EH < EC ( quan hệ đường xuyên đường vuông góc )
Mà E H = EA ( tam giác ABE= tam giác HBE )
câu e) bn chỉ cần chứng minh 3 điểm này thuộc tia phân giác
bài này mk làm rùi!!
56576879870


nếu bạn ko thấy ảnh thì zô thống kê hỏi đáp của mình là thấy bài này nhá . ( cậu tìm câu nào có câu này r ấn zô xem nha )
hoặc link bài của mình nè
https://scontent-hkt1-1.xx.fbcdn.net/v/t1.15752-9/89947717_345887062999332_7304147707155709952_n.jpg?_nc_cat=110&_nc_sid=b96e70&_nc_ohc=Hj57duZ44dcAX91P2ra&_nc_ht=scontent-hkt1-1.xx&oh=7ea184f17776bd230198145c38f92aae&oe=5E95F1D5

Hình tự vẽ
a, \(\Delta BAM\)và \(\Delta BDM\)có
\(\widehat{ABM}=\widehat{DBM}\left(gt\right)\)
\(AM\): cạnh chung
\(\widehat{BAM}=\widehat{BDM}\left(=90^o\right)\)
\(\Rightarrow\Delta BAM=\Delta BDM\left(ch-gn\right)\)
\(\Rightarrow BA=BD\)(2 cạnh tương ứng )
Để nghĩ tiếp :(
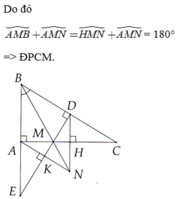
Ta có:
∠AMB+∠ABM=90o
∠BMD+∠MBD=900
Mà ∠AMB=∠BMD (gt)
=> ∠ABM=∠MBD
Xét ΔBAM và ΔBAM có:
∠ABM=∠MBD (gt)
BM chung
∠ABM=∠MBD (cmt)
=> ΔBAM = ΔBAM (g-c-g)
=> BA=BD (2 cạnh tương ứng)
b,Xét ΔABC và ΔDBE có:
∠ABC chung
∠BAC=∠BDM=90o
BA=BD (cmt)
=> ΔABC = ΔDBE (g-c-g)
c,Ta có
BC⊥ED
AK⊥ED
=> BC//AK hay BC//AN
=> ∠ANM=∠MBC ( 2 góc slt) (1)
Mà:
DH⊥AC
BA⊥AC
=> BA//DH hay BA//DN
=> ∠MND=∠ABM ( 2 góc so le trong) (2)
Mà ∠ABM=∠MBD ( vì BM là tia phân giác của góc ABC)
Từ(1) và (2) =>∠ANM=∠MND
=> NM là tia phân giác của góc HMK
d,Ta có BM là tia phân giác của góc ABC (3)
Và NM là tia phân giác của góc HMK
Vì ∠ANM=∠MBC
∠MND=∠ABM
=> ∠ANM=∠MBC=∠MND=∠ABM
=> BN là tia phân giác của góc ABC (4)
Từ (3) và (4) => B,M,N thẳng hàng

a: Xét ΔABE vuông tại A và ΔKBE vuông tại K có
BE chung
ˆABE=ˆKBEABE^=KBE^
Do đó: ΔABE=ΔKBE
b: Xét ΔAEM vuông tại A và ΔKEC vuông tại K cso
EA=EK
ˆAEM=ˆKECAEM^=KEC^
Do đó:ΔAEM=ΔKEC
Suy ra: EM=EC
c: Xét ΔBMC có BA/AM=BK/KC
nên AK//MC