Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=\left(2\cdot R\right)^2-R^2=3\cdot R^2\)
\(\Leftrightarrow AC=R\cdot\sqrt{3}\)(đvđd)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot2R=R\cdot R\sqrt{3}\)
hay \(AH=\dfrac{R\sqrt{3}}{2}\)(đvđd)
Xét ΔABC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{R\sqrt{3}}{2\cdot R}=\dfrac{\sqrt{3}}{2}\)
hay \(\widehat{ABC}=60^0\)
Xét ΔABC vuông tại A có
\(\widehat{ABC}+\widehat{ACB}=90^0\)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}=90^0-60^0\)
hay \(\widehat{ACB}=30^0\)
Vậy: \(AC=R\cdot\sqrt{3}\) đvđd; \(AH=\dfrac{R\sqrt{3}}{2}\)đvđd; \(\widehat{ABC}=60^0\); \(\widehat{ACB}=30^0\)
b) Xét (O) có
BC là đường kính của (O)(gt)
AD là dây của đường tròn(O)
BC⊥AD tại H(gt)
Do đó: H là trung điểm của AD(Định lí đường kính vuông góc với dây)
⇔AH=HD
hay \(AH\cdot HD=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(HB\cdot HC=AH^2\)(2)
Từ (1) và (2) suy ra \(AH\cdot HD=HB\cdot HC\)(đpcm)

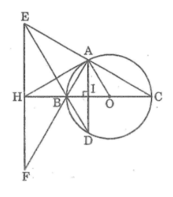

1) Vì BC là đường kính của (O) nên BC=2R
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB^2=BC^2-AC^2=\left(2R\right)^2-R^2=3R^2\)
hay \(AB=R\sqrt{3}\)(đvđd)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot2R=R\cdot R\sqrt{3}\)
\(\Leftrightarrow AH=\dfrac{R^2\cdot\sqrt{3}}{2\cdot R}=\dfrac{R\sqrt{3}}{2}\)(đvđd)
Vậy: \(AB=R\sqrt{3}\); \(AH=\dfrac{R\sqrt{3}}{2}\)
2) Xét (O) có
OC là một phần đường kính
AD là dây
OC⊥AD tại H
Do đó: H là trung điểm của AD(Định lí đường kính vuông góc với dây)
⇒\(HA=HD=\dfrac{AD}{2}\)
hay \(HA\cdot HD=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(HB\cdot HC=AH^2\)(2)
Từ (1) và (2) suy ra \(HA\cdot HD=HB\cdot HC\)(đpcm)
ban co the giup minh 2 y cuoi khong?