Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

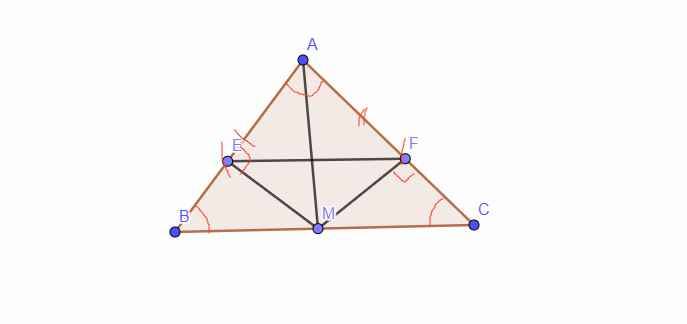
a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

4:
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF
c: AE=AF
ME=MF
=>AM là trung trực của EF
mà K nằm trên trung trực của EF
nên A,M,K thẳng hàng

B E A F C M I 1 2 1 N2
a) M là trung điểm của BC
=> BM=CM
tam giác ABC cân tại A
=> AB=AC
xét tam giác ABM và tam giác ACM có
AB=AC
BM=CM
cạnh AM chung
do đó : tam giác ABM= tam giác ACM ( c.c.c)
b) do tam giác ABM = tam giác ACM
=> góc A1 = góc A2
xét tam giác AEM và tam giác AFM có
cạnh AM chung
góc A1= góc A2
góc AEM=góc AFM =90 độ
do đó tam giác AEM = tam giác AFM ( cạnh huyền - góc nhọn)
c) gọi N là giao của AM va EF
do tam giác AEM= tam giác AFM
=> AE=AF
xét tam giác AEN và tam giác AFN có
cạnh AN chung
góc A1 = góc A2
AE=AF
do đó tam giác AEN=tam giác AFN ( c.g.c)
=> góc N1=góc N2
mà góc N1 + góc N2 = 180 độ ( kề bù)
=> góc N1= góc N2=90 độ
=> AN vuông góc EF
hay AM vuông góc EF
d) Qua F kẻ đg thẳng // với CE cắt AM tại H
+ HF là đg trung bình của ΔACI
⇒HF=\(\frac{1}{2}\)CI⇒HF=12CI
+ ΔABM cân tại M
=> đg cao ME đồng thới là đg trung tuyến
=> AE = BE
+ Tương tự : AF = CF
+ EF là đg trung bình của ΔABC
=> EF // BC
+ Tứ giác EFCM là hbh
=> MK = FK
+ HF // CE => HF // IK
+ IK là đg trung bình của ΔMHF
\(\Rightarrow IK=\frac{1}{2}HF\Rightarrow CI=4IK\)
⇒IK=12HF⇒CI=4IK
a) M là trung điểm của BC
=> BM=CM
tam giác ABC cân tại A
=> AB=AC
xét tam giác ABM và tam giác ACM có
AB=AC
BM=CM
cạnh AM chung
do đó : tam giác ABM= tam giác ACM ( c.c.c)
b) do tam giác ABM = tam giác ACM
=> góc A1 = góc A2
xét tam giác AEM và tam giác AFM có
cạnh AM chung
góc A1= góc A2
góc AEM=góc AFM =90 độ
do đó tam giác AEM = tam giác AFM ( cạnh huyền - góc nhọn)
c) gọi N là giao của AM va EF
do tam giác AEM= tam giác AFM
=> AE=AF
xét tam giác AEN và tam giác AFN có
cạnh AN chung
góc A1 = góc A2
AE=AF
do đó tam giác AEN=tam giác AFN ( c.g.c)
=> góc N1=góc N2
mà góc N1 + góc N2 = 180 độ ( kề bù)
=> góc N1= góc N2=90 độ
=> AN vuông góc EF
hay AM vuông góc EF
hok tốt!

A B C M K Q F E
Xét tam giác ABE và tam giác MBE
có BA=BM(GT)
BE chung
AE=EM (GT)
suy ra tam giác ABE = tam giác MBE (c.c.c)
suy ra góc BEA=góc BEM , góc BAE=góc BME (1)
Mà góc BEA + góc BEM=180độ
suy ra góc BEA =góc BEM=90độ
Xét tam giác EAK và tam giác EMK
có AE=EM (GT)
góc KEA=góc KEM = 90 độ
cạnh EK chung
suy ra tam giác EAK = tam giác EMK (cg.c)
suy ra góc KME=góc KAE (2)
Từ (1) và (2) suy ra góc KME +góc EMB=góc KAE+ góc EAB
suy ra góc KMB=góc KAB = 90 độ
suy ra KM vuông góc với BC
c) sai đề nhé

A B C D E H M
a/ Xét 2 tam giác EMC và tam giác AMB có:
BM=MC (gt)
AM=ME (gt)
Góc AMB=góc EMC (2 góc đối đỉnh)
=> tam giác EMC = tam giác AMB (Cạnh-góc-cạnh)
=> AB=EC (2 cạnh tương ứng)
b/ Xét tam giác ADE có:
AH=HD (gt)
AM=ME (gt)
=> HM là đường trung bình của tam giác ADE => HM//DE => AD vuông góc DE (1)
và DE/2=HM (Tính chất đường trung bình)
Mà DF=FE=DE/2
=> DF=HM=DE/2 (2)
Từ (1) và (2) => Tứ giác HMFD là hình chữ nhật => MF vuông góc DE
c/ MF//DH (cmt)
=> MF//AD

a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b:Sửa đề: Chứng minh AE=AF
Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
nên EF//BC
d: Xét ΔABN vuông tại B và ΔACN vuông tại C có
AN chung
AB=AC
Do đó: ΔABN=ΔACN
=>BN=CN
=>N nằm trên đường trung trực của BC(1)
Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,M,N thẳng hàng
áp dụng tính đường trung bình của tam giác đấy bạn!!!