Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEBF có
D là trung điểm của AB
D là trung điểm của EF
Do đó: AEBF là hình bình hành
b: Xét tứ giác ABFO có
AO//BF
AO=BF
Do đó: ABFO là hình bình hành
mà \(\widehat{BAO}=90^0\)
nên ABFO là hình chữ nhật

a: Xét tứ giác ABKC có
M là trung điểm chung của AK và BC
AB=AC
Do đó: ABKC là hình thoi
b: Để ABKC là hình vuông thì góc BAC=90 độ
c: Xét tứ giác ABCD có
AB//CD
AD//BC
=>ABCD là hình bình hành
=>AD=BC

a) Ta có AD = 1 2 B C = 8 2 = 4 c m
Xét DADC có GF là đường trung bình
⇒ G F = 1 2 A D = 4 2 = 2 c m
b) Chứng minh ADCE là hình thoi. Để ADCE là hình vuông thì điều kiện cần và đủ là E C D ^ = 90 0 ⇔ C 1 ^ = C 2 ^ = 45 0
Û DABC vuông tại A.
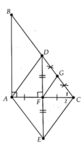
b: \(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{3\cdot4}{2}=6\left(cm^2\right)\)
Bn bt làm 2 câu còn lại ko ạ🙂