Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tam giác MAH và tam giác MBA
Có: góc MHA = góc MAB=90 độ
góc BMA chung
Do đó : tam giác MAH đồng dạng với tam giác MBA ( gg)
a)xét tam giác MAH và tam giác MBA có:
góc BMA chung
góc BAM=góc AHM=90 độ
\(\Rightarrow\)tam giác BAM~tam giác AHM(g.g)
b)theo câu a) ta có:
\(\dfrac{AM}{MB}=\dfrac{AH}{AB}=\dfrac{MH}{MA}\left(1\right)\)
ta có :
\(AM=MCnên\dfrac{AM}{MB}=\dfrac{MC}{MB}\left(2\right),\dfrac{MH}{MA}=\dfrac{MH}{MC}\left(3\right)\)
từ (1), (2), (3) \(\Rightarrow\dfrac{MC}{MB}=\dfrac{MH}{MC}\left(=\dfrac{AH}{AB}\right)\)
tam giác MHC và tam giác MCB có:
\(\dfrac{MC}{MB}=\dfrac{MH}{MC}\) (cmt)
góc BMC chung
\(\Rightarrow\)tam giác MHC ~ tam giác MCB(c.g.c)
\(\Rightarrow\) góc BCM=gócCHM

a: Xét ΔBHI vuông tại H và ΔAKI vuông tại K có
góc BIH=góc AIK
=>ΔBHI đồng dạng vói ΔAKI
=>IB*IK=IA*IH
b: góc BHA=góc BKA=90 độ
=>BHKA nội tiếp
=>góc BAH=góc BKH

a: Xét ΔEAC vuông tại A và ΔEDB vuông tại D có
\(\widehat{AEC}\) chung
Do đó: ΔEAC đồng dạng với ΔEDB
b: Ta có: ΔEDB vuông tại D
=>\(\widehat{DEB}+\widehat{DBE}=90^0\)
=>\(\widehat{DEB}=60^0\)
Xét ΔEDB vuông tại D có \(cosE=\dfrac{ED}{EB}\)
=>\(\dfrac{ED}{EB}=cos60=\dfrac{1}{2}\)
Ta có: ΔEAC đồng dạng với ΔEDB
=>\(\dfrac{EA}{ED}=\dfrac{EC}{EB}\)
=>\(\dfrac{EA}{EC}=\dfrac{ED}{EB}\)
Xét ΔEAD và ΔECB có
EA/EC=ED/EB
góc E chung
Do đó: ΔEAD đồng dạng với ΔECB
=>\(\dfrac{S_{EAD}}{S_{ECB}}=\left(\dfrac{ED}{EB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ECB}=50\cdot4=200\left(cm^2\right)\)

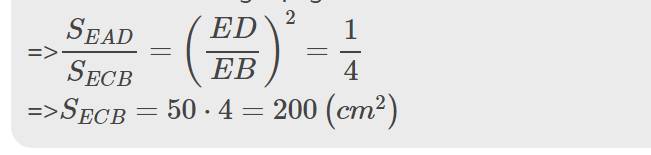
a: Xét ΔMAH vuông tại H và ΔMBA vuông tại A có
góc HMA chung
Do đó:ΔMAH\(\sim\)ΔMBA
b: Xét ΔMAB vuông tại A có AH là đường cao
nên \(MA^2=MH\cdot MB\)
\(\Leftrightarrow MC\cdot MC=MH\cdot MB\)
hay MC/MH=MB/MC
Xét ΔMCB và ΔMHC có
MC/MH=MB/MC
góc CMB chung
Do đó: ΔMCB\(\sim\)ΔMHC
Suy ra: \(\widehat{BCM}=\widehat{CHM}\)