Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
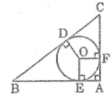
Gọi E và F lần lượt là tiếp điểm của đường tròn với AD và AC
Theo tính chất hai tiếp tuyến cắt nhau, ta có:
AE = AF
BE = BD
CD = CF
BD = BC + CD
BE = AB – AE
Suy ra: BD + BE = AB + BC – (AE + CD)
= AB + BC – (AE + CE)
= AB + BC – AC
Suy ra: BD = (AB + BC - AC)/2
Lại có: CD = BC – BD
CF = AC = AF
Suy ra: CD + CF = BC + AC – (BD + AF)
= BC + AC – (BE + AE)
= BC + AC – BA
Vậy S A B C = BD.DC.
Đặt BC = a , AC = b , AB = c . Ta có :
\(BD=\frac{a+c-d}{2}\)
\(DC=\frac{a+b-c}{2}\)
Do đó , ta giả sử \(\left(b\ge c\right)\)
\(BD.DC=\frac{a+c-b}{2}.\frac{a+b-c}{2}\)
\(=\frac{a-\left(b-c\right)}{2}.\frac{a+\left(b-c\right)}{2}\)
\(=\frac{a^2-\left(b-c\right)^2}{4}\)
\(=\frac{a^2-b^2+2bc-c^2}{4}\)
\(=\frac{a^2-\left(b^2+c^2\right)+2bc}{4}\)
Do \(a^2=b^2+c^2\)nên \(BD.DC=\frac{2bc}{3}=\frac{bc}{2}=S_{ABC}\)
Ta chỉ cần chứng minh \(BD=CE.\) (Thực vậy, khi đó nếu I là trung điểm BC thì BI=EI).
Để cho tiện ta kí hiệu \(a=BC,b=CA,c=AB.\)
Gọi \(D,P,Q\) là tiếp điểm của đường tròn nội tiếp với ba cạnh \(BC,CA,AB.\)
Gọi \(E,R,S\) là tiếp điểm của đường tròn bàng tiếp góc A với ba cạnh \(BC,CA,AB.\)
Ta có \(BD=BQ,CR=CD,AQ=AR\Rightarrow BD+CR+AQ=\frac{a+b+c}{2}\)
Mặt khác \(AR+CR=b\Rightarrow BD=\frac{a+c-b}{2}\). (1)
Theo tính chất tiếp tuyến
\(2AR=AR+AS=AB+AC+BS+CR=AB+AC+BC\Rightarrow AR=\frac{a+b+c}{2}.\)
Do đó \(CE=CR=AR-AC=\frac{a+b+c}{2}-b=\frac{a+c-b}{2}.\) (2)
Từ (1),(2) suy ra \(BD=CE\).
Pitago: \(BC^2=AB^2+AC^2\Rightarrow BC^2-\left(AB^2+AC^2\right)=0\)
Gọi các tiếp điểm với AB và AC là E và F
Do đường tròn (I) nội tiếp tam giác, theo t/c hai tiếp tuyến cắt nhau:
\(BD=BE\) ; \(AE=AF\) ; \(CD=CF\)
Mà \(BD+CD=BC;AE+BE=AB;AF+CF=AC\)
\(\Rightarrow BC+AB-AC=BD+CD+AB+BE-AF-CF=BD+BE=2BD\)
\(\Rightarrow BD=\dfrac{BC+AB-AC}{2}\)
Tương tự: \(BC+AC-AB=2DC\Rightarrow DC=\dfrac{BC+AC-AB}{2}\)
\(\Rightarrow BD.DC=\dfrac{1}{4}\left(BC+AB-AC\right)\left(BC+AC-AB\right)=\dfrac{1}{4}\left[BC^2-\left(AB-AC\right)^2\right]\)
\(=\dfrac{1}{4}\left(BC^2-\left(AB^2+AC^2\right)+2AB.AC\right)=\dfrac{1}{2}AB.AC=S_{ABC}\)