Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

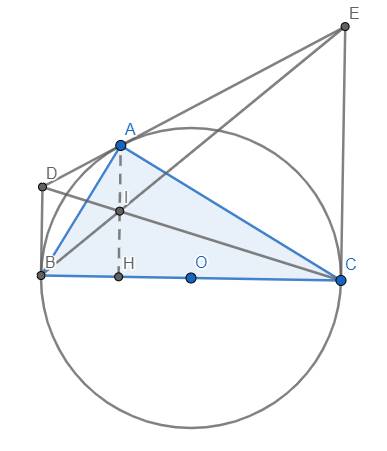
a) Theo tính chất của 2 tiếp tuyến cắt nhau \(\left\{{}\begin{matrix}AD=BD\\AE=CE\end{matrix}\right.\)
\(\Rightarrow\dfrac{AD}{AE}=\dfrac{BD}{CE}=\dfrac{ID}{IC}\)
\(\Rightarrow\) AI//CE.
Mà \(CE\perp BC\) nên \(AI\perp BC\)
Lại có \(AH\perp BC\) \(\Rightarrow\) A, I, H thẳng hàng (đpcm)
b) Theo định lý Thales, ta có \(\dfrac{AI}{CE}=\dfrac{DA}{DE}\) và \(\dfrac{IH}{CE}=\dfrac{BH}{BC}\)
Mặt khác, \(\dfrac{DA}{DE}=\dfrac{BH}{BC}\) (đl Thales trong hình thang)
\(\Rightarrow\dfrac{AI}{CE}=\dfrac{IH}{CE}\) \(\Rightarrow AI=IH\) (đpcm)
c) Ta có \(\dfrac{DB}{DE}=\dfrac{DA}{DE}=\dfrac{AI}{CE}\) \(\Rightarrow DB.CE=DE.AI\) (đpcm)

a: Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: AH⊥BC
hay AF⊥BC

A B C D H F E I L S G K M U V
Gọi I là giao của BF và CE, đường tròn (HEF) cắt BC tại S khác H. Vẽ (B;BA) và (C;CA) cắt nhau tại M khác A
Kéo dài BD cắt (C) tại G khác E, CD cắt (B) tại K khác F. Dễ thấy A,H,M thẳng hàng nên ta có:
DF.DK = DA.DM = DE.DG do đó 4 điểm E,F,G,K đồng viên
Ta có BF2 = BA2 = BE.BG suy ra \(\Delta\)BEF ~ \(\Delta\)BFG (c.g.c). Tương tự \(\Delta\)CEF ~ \(\Delta\)CKE (c.g.c)
Từ đó ^BFE = ^BGF = ^CKE = ^CEF, suy ra \(\Delta\)EIF cân tại I
Gọi BF,CE cắt (HEF) lần lượt tại U,V. Dễ có SV // BE, SU // CF và FU = EV (Vì IE = IF)
Ta lại có \(BH.BS=BU.BF;CH.CS=CV.CE\Rightarrow\frac{BS}{CS}.\frac{BH}{CH}=\frac{BF}{CE}.\frac{BU}{CV}\)
Hay \(\frac{BS}{CS}.\frac{AB^2}{AC^2}=\frac{AB}{AC}.\frac{BU}{FU}.\frac{EV}{CV}=\frac{AB}{AC}.\frac{BS^2}{CS^2}\Rightarrow\frac{AB}{AC}=\frac{BS}{CS}\)
Suy ra S là chân đường phân giác trong kẻ từ đỉnh A của tam giác ABC
Vì vậy S cố định, khi đó đường tròn (HEF) đi qua hai điểm H,S cố định
Vậy thì tâm L của đường tròn (HEF) luôn thuộc trung trực của SH cố định (đpcm).