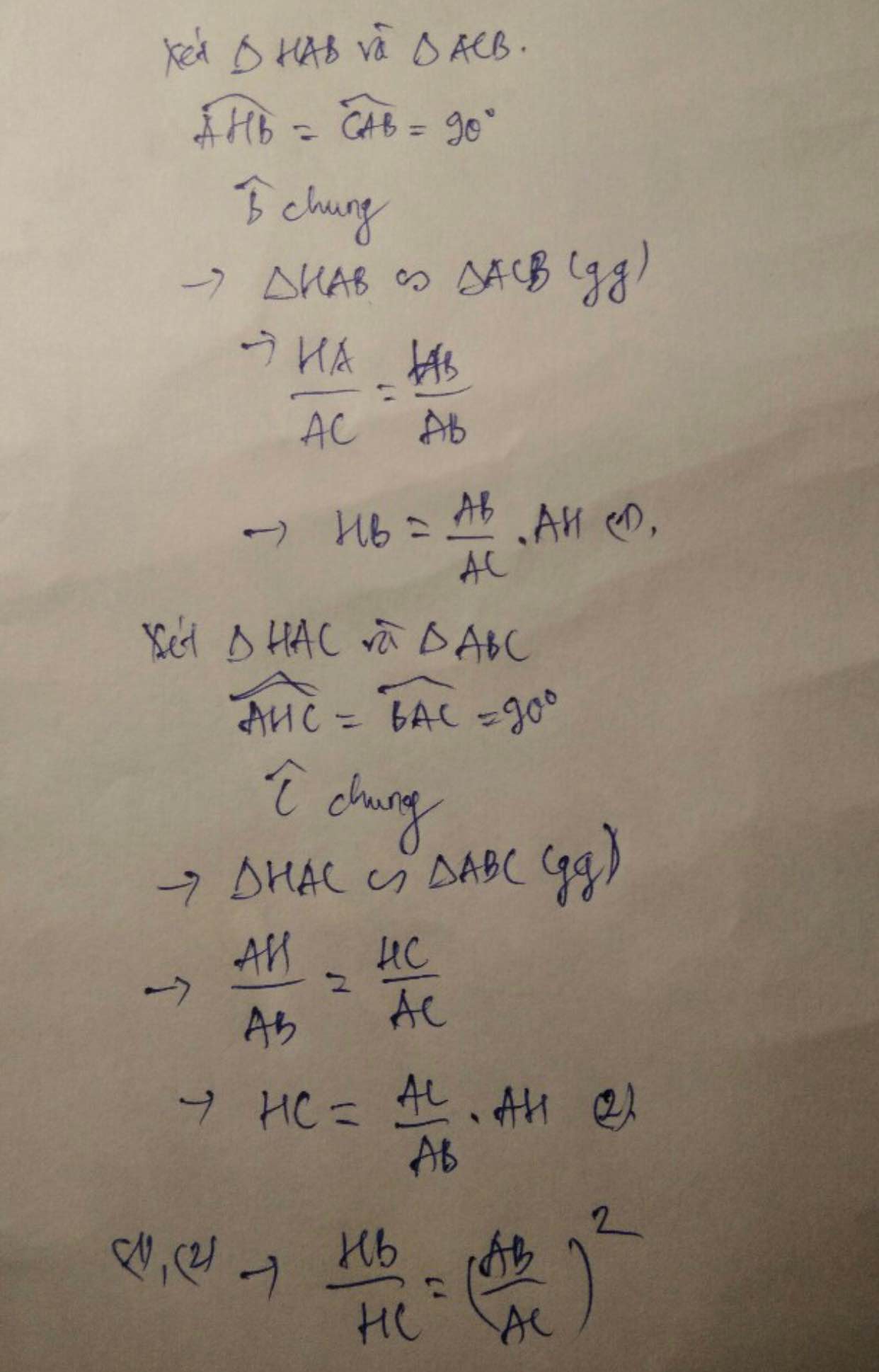Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC vuông tại A, đường cao AH.Gọi M,N lần lượt là trung điểm của AC và HC
c/m HB.HC=4MN2

Lời giải:
Áp dụng hệ thức lượng trong tam giác vuông cho tam giác $ABC$ vuông tại $A$, đường cao $AH$:
$HB.HC=AH^2(1)$
Mặt khác:
$M,N$ là trung điểm $AC,HC$ nên $MN$ là đường trung bình của tam giác $AHC$ ứng với cạnh $AH$
$\Rightarrow MN=\frac{1}{2}AH$ hay $AH=2MN(2)$
Từ $(1);(2)\Rightarrow HB.HC=AH^2=(2MN)^2=4MN^2$
Ta có đpcm.

Truc Nguyen nè, nếu bạn không giải được cho người ta thì đừng có giải nhé, giải mà toàn chửi không thì ai mà hiểu, xem tôi giải nè:
a) Xét \(\Delta ABC\) vuông tại A, đường cao AH, ta có:
BC2=AB2+AC2( định lí Pytago)
\(\Leftrightarrow\)BC=\(\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=\sqrt{81+144}=\sqrt{225}=15\left(cm\right)\)
AH.BC=AB.AC( hệ thức về cạnh và đường cao trong tam giác vuông)
\(\Leftrightarrow\)AH= \(\dfrac{AB.AC}{BC}=\dfrac{9+12}{15}=9.8\left(cm\right)\)
b) Xét \(\Delta AHB\) có HD là đường cao:
\(AH^2=AD.AB\) ( hệ thức trong tam giác vuông) (1)
Xét \(\Delta AHC\) có HE là đường cao:
\(AH^2=AE.AC\) ( hệ thức trong tam giác vuông) (2)
Từ (1) và (2) suy ra: AD.AB = AE.AC
c) Gọi M và N lần lượt là trung điểm của AC và HC
Ta có:
NE = EC (M là trung điểm của AC)
HN = NC( N là trung điểm của HC)
Suy ra: MN là đường trung bình của \(\Delta AHC\)
\(\Rightarrow MN=\dfrac{1}{2}AH\Rightarrow AH=2MN\)
Xét \(\Delta ABC\) có góc A = \(90^o\), AH là đường cao
\(AH^2=BH.HC\) ( hệ thức trong tam giác vuông)
Do đó:(2MN)2 = BH.HC
hay 4MN = BH.HC ( điều phải chứng minh)
Vậy BH.HC=4MN
Truc Nguyen nè, bớt ngay cái tật kiêu căng không coi ai ra gì đi nhé, chuyện của bạn ấy có mướn bạn nói không mà sao bạn nói nhiều vậy? Biết phận mình giỏi rồi mà thích khinh người thì tránh ra đi nhé, bạn ấy học yếu thì để bạn ấy học đi chứ, cứ sấn vào chửi không à, dai còn hơn cả đỉa, có ai khinh người mà cứ thích sấn vào chửi người khác không? Chỉ có mấy thằng điên con điên mới thích sấn vào chửi thôi nhé. Lo việc mình trước khi lo việc thiên ha đi nhé, lo việc thiên hạ nhiều có ngày bị người ta đánh cho thì khổ ra đấy.

A B C H M N
Ta có : \(AB^2=BH.BC\)
\(AC^2=CH.BC\)
Chia vế với vế ta được :
\(\dfrac{AB^2}{AC^2}=\dfrac{BH.BC}{CH.BC}\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{BH}{CH}\)

Cho tam giác ABC vuông tại A( AB<AC ), có đường cao AH, trung tuyến AM Gọi E và F lần lượt la hình chiếu của H lên AB và AC; I và K lần lượt là trung điểm của HB và HC. CM :