Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B1: Gọi Tam giác ABC vuông tại A có AH là đ/cao chia cạnh huyền thành 2 đoạn HB và HC
AH2=HB x HC =3x4=12
AH=căn 12 r tính mấy cạnh kia đi
B2: Ta có AB/3=AC/4 suy ra AB = 3AC/4
Thế vào cong thức Pytago Tam giác ABC tính máy cái kia

\(HC-HB=9\Rightarrow HC=HB+9\)
Áp dụng hệ thức lượng:
\(AH^2=HB.HC\Leftrightarrow6^2=HB\left(HB+9\right)\)
\(\Leftrightarrow HB^2+9HB-36=0\Rightarrow\left[{}\begin{matrix}HB=3\\HB=-12\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow HC=HB+9=12\)
Ta có: HC-HB=9
nên HC=9+HB
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB^2+9HB-36=0\)
\(\Leftrightarrow\left(HB+12\right)\left(HB-3\right)=0\)
\(\Leftrightarrow HB=3\left(cm\right)\)
\(\Leftrightarrow HC=12\left(cm\right)\)

\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
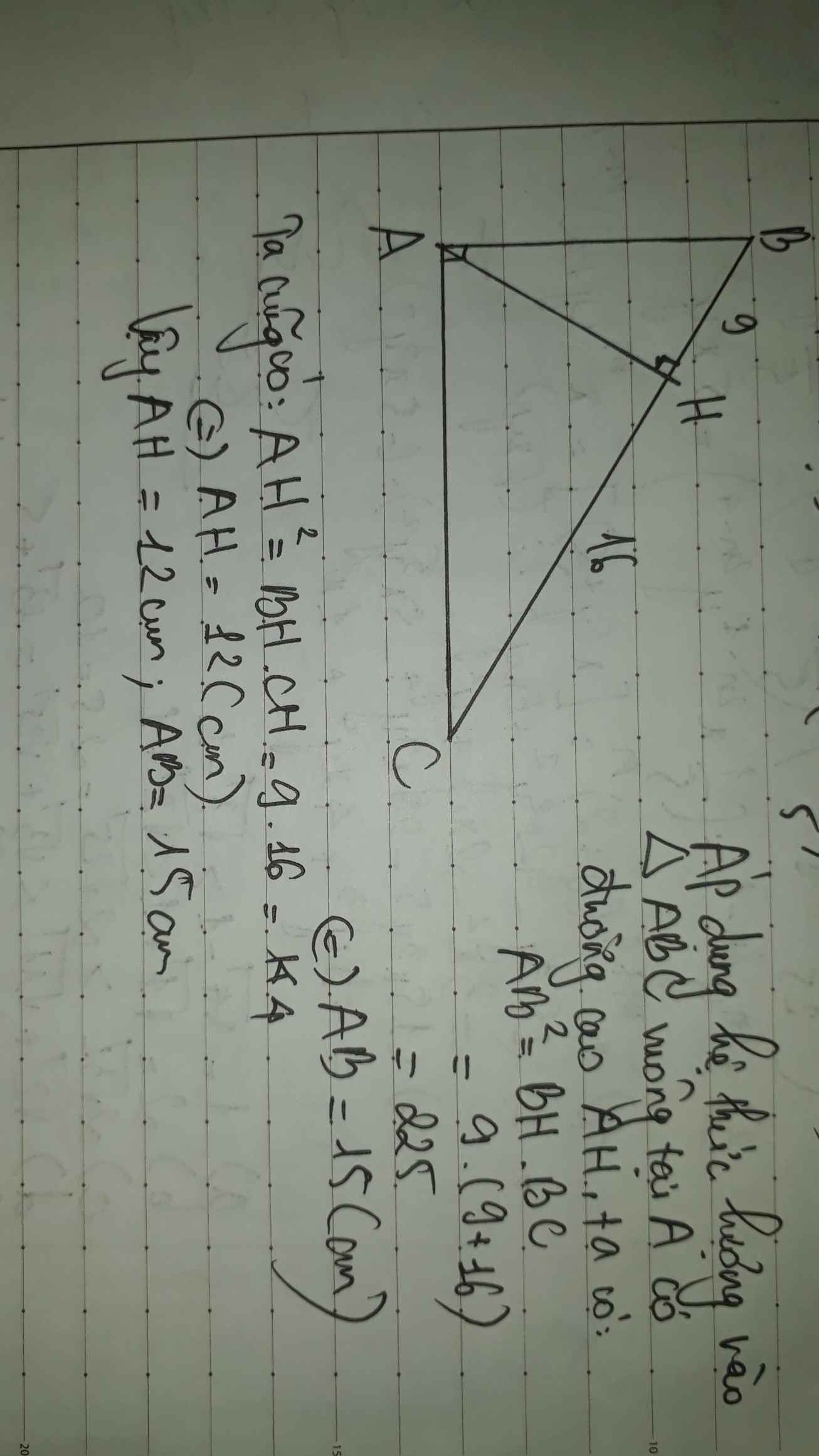
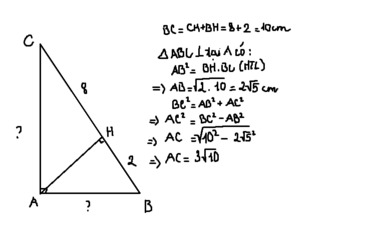
Ta có: BC = HC + HB = 18 + 32 = 50 (cm)
Xét tam giác ABC vuông tại A, đường cao AH, ta có:
AB = \(\sqrt{BC.BH}=\sqrt{50.32}=40\)(cm)
AC = \(\sqrt{BC.HC}=\sqrt{50.18}=30\)(cm)
AH = \(\sqrt{BH.CH}=\sqrt{32.18}=24\)(cm)
=> Tam giác ABC có độ dài 3 cạnh là AB = 40cm; AC = 30cm; BC = 50cm và đường cao AH = 24cm