Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của đoàn kiều oanh - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!

-Lưu ý: Chỉ mang tính chất tóm tắt bài làm, bạn không nên trình bày theo nhé!
a) △ABD và △EBD có: \(\widehat{ABD}=\widehat{EBD}\) (BD là tia phân giác của \(\widehat{ABC}\)) ; BD là cạnh chung ; \(\widehat{BAD}=\widehat{BED}=90^0\)
\(\Rightarrow\)△ABD=△EBD (c-g-c).
b) △ABD=△EBD (cmt) \(\Rightarrow AB=EB\) \(\Rightarrow\)△ABE cân tại B mà \(\widehat{ABC}=60^0\)
\(\Rightarrow\)△ABE đều.
c) \(\widehat{BAE}+\widehat{EAC}=90^0\Rightarrow60^0+\widehat{EAC}=90^0\Rightarrow\widehat{EAC}=30^0\)
\(\widehat{ABE}+\widehat{ACE}=90^0\Rightarrow60^0+\widehat{ACE}=90^0\Rightarrow\widehat{ACE}=30^0=\widehat{EAC}\)
\(\Rightarrow\)△AEC cân tại E. \(\Rightarrow AE=EC=AB=BE\)
\(\Rightarrow\)E là trung điểm BC và \(AB=\dfrac{1}{2}BC\)
\(\Rightarrow BC=10 \left(cm\right)\)

a) Tam giác ABD vuông và tam giác EBD vuông đều có cạnh BD
Suy ra góc ABD = góc EBD
Vậy tam giác ABD = tam giác EBD
b) Ta có: AB=EB ( tam giác ABD = tam giác EBD )
Suy ra tam giác ABE cân tại B
Tam giác ABE cân tại B có góc EBA =60 độ
Suy ra tam giác ABE là tam giác đều
c) Tam giác ABC có góc CAB = 90 độ, góc CBA = 60 độ
Suy ra ACB = 30 độ
Suy ra tam giác ABC là nửa tam giác đều
Suy ra AB = 1/2 BC
Suy ra BC = 2AB = 2 . 5 = 10 cm
-Tham khảo-
a, Xét tam giác ABD và tam giác EBD có :
BD chung
góc ABD = góc EBD ( vì BD là phân giác của ABC)
=> tam giác ABD=tam giác EBD ( cạnh huyền-góc nhọn)
b, Vì tam giác ABD= tam giác EBD ( câu a)
=> AB=EB
Xét tam giác ABE có :
AB=EB
=> Tam giác ABE cân tại B
Xét tam giác ABE cân tại B có :
ABE =60 độ( vì góc ABC=60 độ)
=> Tan giác ABE đều
c, Xét tam giác ABC vuông tai jS có :
góc ABC =60 độ ( giả thiết), góc BAC= 90 độ( Vì tam giác ABC vuông tại A)
=> góc C = 30 độ
Mà trong tam giác vuông , cạnh đối diện với góc 30 độ bằng nửa cạnh huền
=> 2AB = BC . Mà AB = 5 ( giả thiết)
=> BC =10
Áp dụng định lý PYTAGO vào tam giác ABC vuông tại A có :
BC^2 = AB^2 + AC^2 . Mà AB = 5 , BC =10
=> 10^2 = 5^2 + AC^2
=> 100=25 + AC^2
=> AC^2 = 75
=> AC = căn bậc 2 của 75 ( Vì mình ko đánh dấu căn bậc 2 được nên đành phải viết)
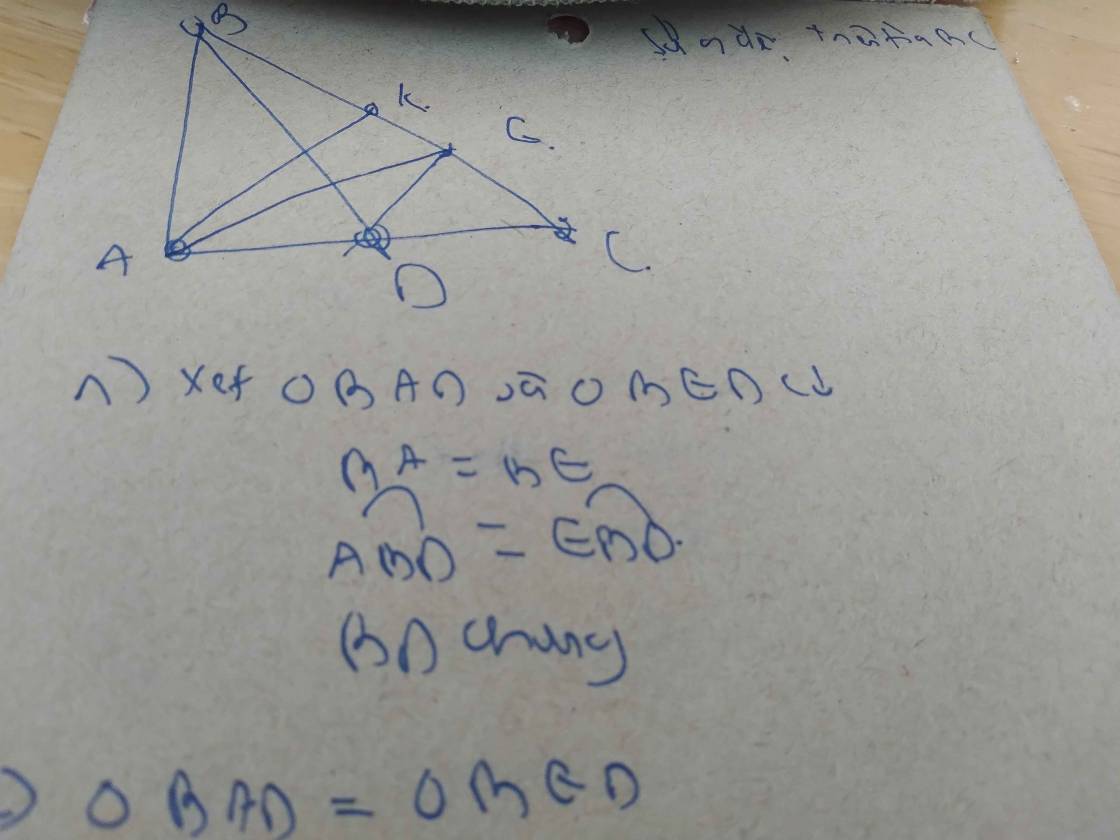

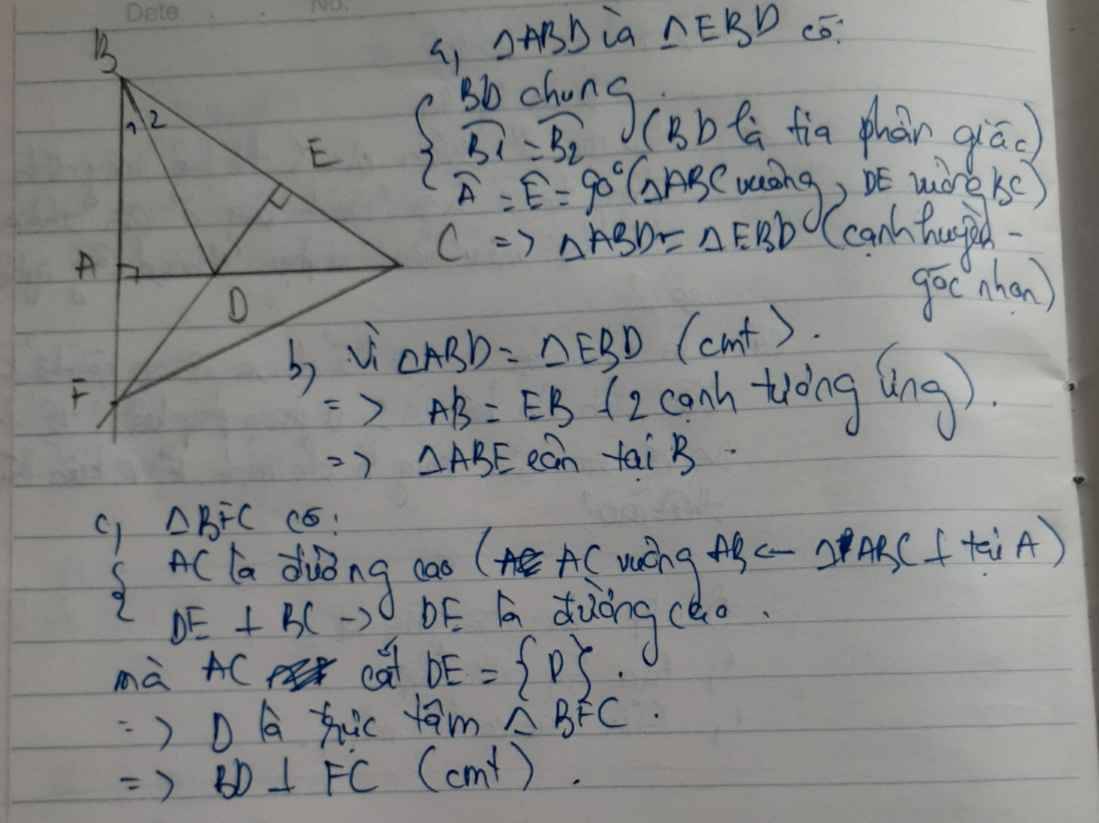
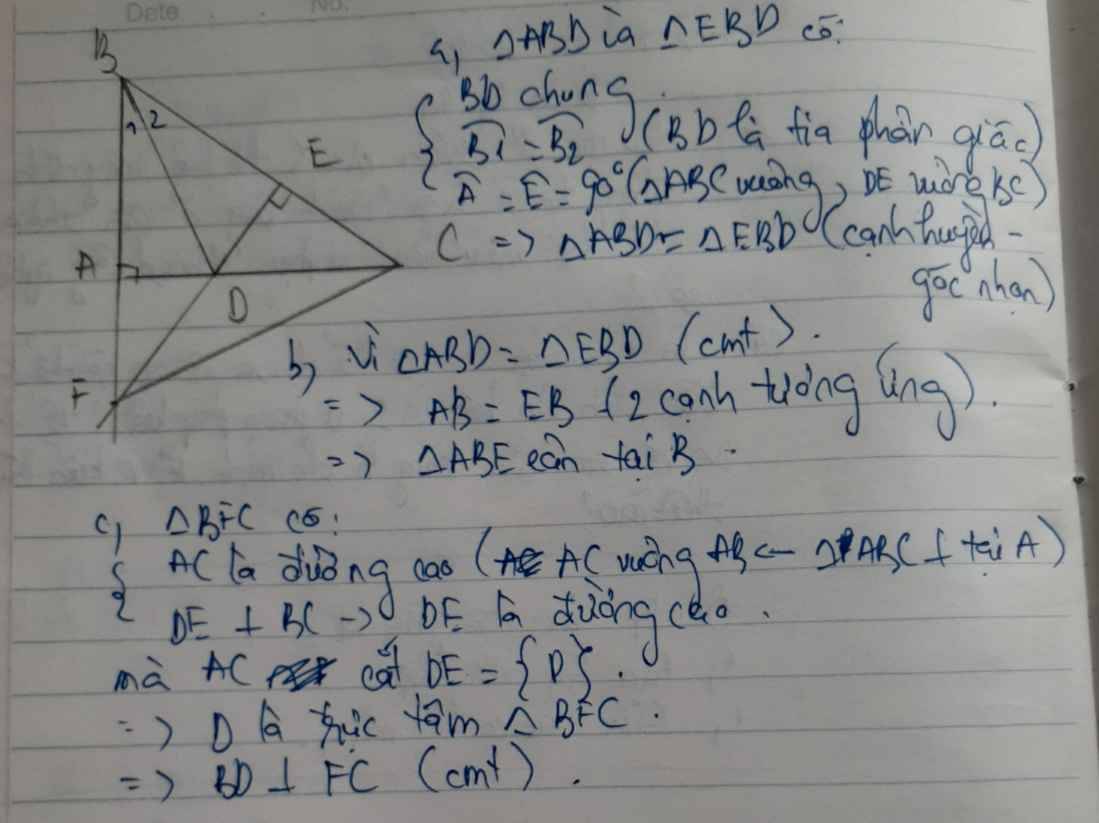
hình như bạn thiếu đề hay sao đấy
Bạn tự vẽ hình và ghi giả thiết kết luận nhé
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có :
BD : cạnh chung
Góc ABD = góc EBD (gt)
Do đó : Tam giác ABD = tam giác EBD
=> BA = BE (hai cạnh tương ứng) (Đccm)
Gọi I là giao điểm của BD và AE.
Vì tam giác ABD = tam giác EBD
=> Góc BED = góc ABD ( hai góc tương ứng)
Xét tam giác BIE và tam giác BIA có:
BA = BE (cmt)
Góc EBI = ABI (gt)
BI là cạnh chung
Do đó : tam giác BIE = tam giác BIA (c.g.c)
=> Góc BEI = góc ABI (hai góc tương ứng)
=> Tam giác ABE là tam giác cân tại B (vì có 2 góc ở đày bằng nhau)
mà góc EBA = 60o
=> Tam giác ABE là tam giác đều (Đccm)
* CM E là trung điểm của BC
Ta có :Góc ABE = 60 độ
mà BD là tia phân giác của góc A
=> Góc ABD = góc EBD = 60 độ /2 = 30 độ
Xét tam giác BED vuông tại E có:
Góc EBD + góc BDE = 90 độ
30 độ + góc BDE = 90 độ
Góc BDE =90-30=60 độ
Xét tam giác BAD vuông tại A có:
Góc ABD + góc BDA = 90 độ
30 độ + góc BDA = 90 độ
Góc BDA =90-30=60 độ
Ta có : Góc ADB + góc BDE + góc EDC = 180 độ
60 + 60 + góc EDC = 180 độ
Góc EDC = 180 -60-60 =60 độ
Xét tam giác BDE và tam giác CDE đều vuông tại E có :
DE: cạnh chung
Góc BDE = góc CDE (cmt)
Do đó : tam giác BDE = tam giác CDE (cạnh huyền - góc nhọn)
=>BE = CE (hai cạnh tương ứng )
=>E là trung điểm của BC (đccm)