Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: F là hình chiếu của E trên AC
a: Xét ΔCAB có
E là trung điểm của CB
EF//AB
=>F là trung điểm của AC
Xét ΔCAB có
E là trung điểm của CB
ED//AC
=>D là trung điểm của AB
Xét ΔABC có EF//AB
nên EF/Ab=CE/CB=1/2
=>EF=1/2AB=DB
Xét tứ giác BDFE có
FE//BD
FE=BD
=>BDFE là hình bình hành
b: Xét ΔABC có AD/AB=AF/AC
nên DF//BC
=>DF//EH
ΔHAC vuông tại H có HF là trung tuyến
nên HF=AC/2
=>HF=ED
Xét tứ giác EHDF có
EH//DF
ED=HF
=>EHDF là hình thang cân
c: Xét tứ giác ABCN có
F là trung điểm chung của AC và BN
=>ABCN là hình bình hành
=>AN//CB
Xét tứ giác AMCE có
F là trung điểm chung của AC và ME
=>AMCE là hình bình hành
=>AM//CE
=>AM//CB
mà AN//CB
nên A,N,M thẳng hàng

a: Sửa đề: EF vuông góc AC
Xét ΔABC có
E là trung điểm của BC
EF//AB
=>F là trung điểm của AC
Xét ΔABC có
E là trung điểm của BC
ED//AC
=>D là trung điểm của AB
=>BD//FE và BD=FE
=>BDFE là hình bình hành
b: Xét ΔABC có AD/AB=AF/AC
nên DF//BC
=>DF//EH
ΔHAC vuông tại H có HF là trung tuyến
nên HF=AC/2=ED
Xét tứ giác EHDF có
EH//DF
ED=FH
=>EHDF là hình thang cân

Để chứng minh ADEF là hình chữ nhật, ta cần chứng minh các đẳng thức đường cao AH = trung tuyến AE và hình chiếu D, F của E trên AB, AC vuông góc với AB, AC.
a) Chứng minh AH = AE: Vì tam giác ABC là tam giác vuông tại A, nên đường cao AH cũng là đường cao của tam giác vuông ABC. Do đó, ta có AH = BH. Từ tam giác ABC, ta có AE là trung tuyến nên AE = EC. Vậy, AH = AE.
b) Chứng minh AD = AF: Ta có hai tam giác vuông ADE và AFE có cạnh chung AE. Vì AE là trung tuyến nên ta có DE = FE, và góc ADE = góc AFE = 90 độ (do DE và FE vuông góc với AB, AC). Do đó, ta có hai tam giác ADE và AFE đồng dạng (cạnh góc). Từ đó suy ra, AD = AF.
Vì AH = AE và AD = AF, nên tứ giác ADEF là hình chữ nhật.
c) Chứng minh BDFE là hình bình hành: Ta đã chứng minh được AD = AF, nên BD = BF (do AB < AC). Vì DE = EF (vì trung tuyến), và góc EDF = góc EBF = 90 độ (hình chiếu của E trên AB, AC vuông góc với AB, AC), nên ta có hai cạnh và một góc tương đương nhau. Do đó, tứ giác BDFE là hình bình hành.
d) Chứng minh F là trung điểm của AC: Vì AE là trung tuyến của tam giác ABC, nên F là trung điểm của AC.
Vậy, ta đã chứng minh được các yêu cầu đề bài.

A B C E F H I M G N P Q K
Gọi P là giao của BN với EH; Q là giao của MN với HF; K là giao của MN với EF
Ta có
\(EH\perp BC;AI\perp BC\)=> EH//AI \(\Rightarrow\frac{PE}{NA}=\frac{PH}{NI}\) (Talet) \(\Rightarrow\frac{PE}{PH}=\frac{NA}{NI}=1\Rightarrow PE=PH\)
=> BN đi qua trung điểm P của EH
Ta có
EF//BC (gt) => KF//HM \(\Rightarrow\frac{QK}{QM}=\frac{QF}{QH}=\frac{KF}{HM}\) (Talet) => KH//FM
Xét tứ giác KFMH có
KF//HM; KH//FM => KFMH là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> KF=HM (Trong hình bình hành các cạnh đối bằng nhau)
\(\Rightarrow\frac{QF}{QH}=\frac{KF}{HM}=1\Rightarrow QF=QH\)
=> MN đi qua trung điểm Q của HF

Bài 1:
A B C D M N P Q E F
a) Xét tam giác ABC có M là trung điểm của AB (gt) ,E là trung điểm của AC (gt)
\(\Rightarrow ME\)là đường trung bình tam giác ABC
\(\Rightarrow ME=\frac{1}{2}BC\left(tc\right)\left(1\right)\)
Xét tam giác ADC có E là trung điểm của AC (gt) ,P là trung điểm của DC (gt)
\(\Rightarrow PE\)là đường trung bình của tam giác ADC
\(\Rightarrow PE=\frac{1}{2}AD\left(tc\right)\left(2\right)\)
mà \(AD=BC\left(gt\right)\left(3\right)\)
Từ (1) , (2) và (3) \(\Rightarrow EM=PE\)
CMTT: \(PE=FP,FM=ME\)
\(\Rightarrow ME=EP=PF=FM\)
Xét tứ giác MEPF có:
\(ME=EP=PF=FM\left(cmt\right)\)
\(\Rightarrow MEPF\)là hình thoi ( dhnb)
b) Vì \(MEPF\)là hình thoi (cmt)
\(\Rightarrow FE\)giao với MP tại trung điểm mỗi đường (tc) (4)
Xét tam giác ADB có M là trung điểm của AB(gt) ,Q là trung điểm của AD (gt)
\(\Rightarrow MQ\)là đường trung bình của tam giác ADB
\(\Rightarrow MQ//DB,MQ=\frac{1}{2}DB\left(tc\right)\left(5\right)\)
Xét tam giác BDC có N là trung điểm của BC(gt) , P là trung điểm của DC(gt)
\(\Rightarrow NP\)là đường trung bình của tam giác BDC
\(\Rightarrow NP//DB,NP=\frac{1}{2}DB\left(tc\right)\left(6\right)\)
Từ (5) và (6) \(\Rightarrow MQ//PN,MQ=PN\)
Xét tứ giác MQPN có \(\Rightarrow MQ//PN,MQ=PN\)
\(\Rightarrow MQPN\)là hình bình hành (dhnb)
\(\Rightarrow MP\)giao QN tại trung điểm mỗi đường (tc) (7)
Từ (4) và (7) \(\Rightarrow MP,NQ,EF\)cắt nhau tại một điểm
c) Xét tam giác ABD có Q là trung điểm của AD (gt), F là trung điểm của BD(gt)
\(\Rightarrow QF\)là đường trung bình của tam giác ADB
\(\Rightarrow QF//AB\left(8\right)\)
CMTT: \(FN//CD\)và \(EN//AB\)
Mà Q,F,E,N thẳng hàng
\(\Rightarrow AB//CD\)
Vậy để Q,F,E,N thẳng hàng thì tứ giác ABCD phải thêm điều kiện \(AB//CD\)

"trên tia đối của tia EH lấy điểm P ..." bài này có sai đề không nhỉ, không thể tồn tại hai điểm P, Q thì làm sao vẽ hình được e
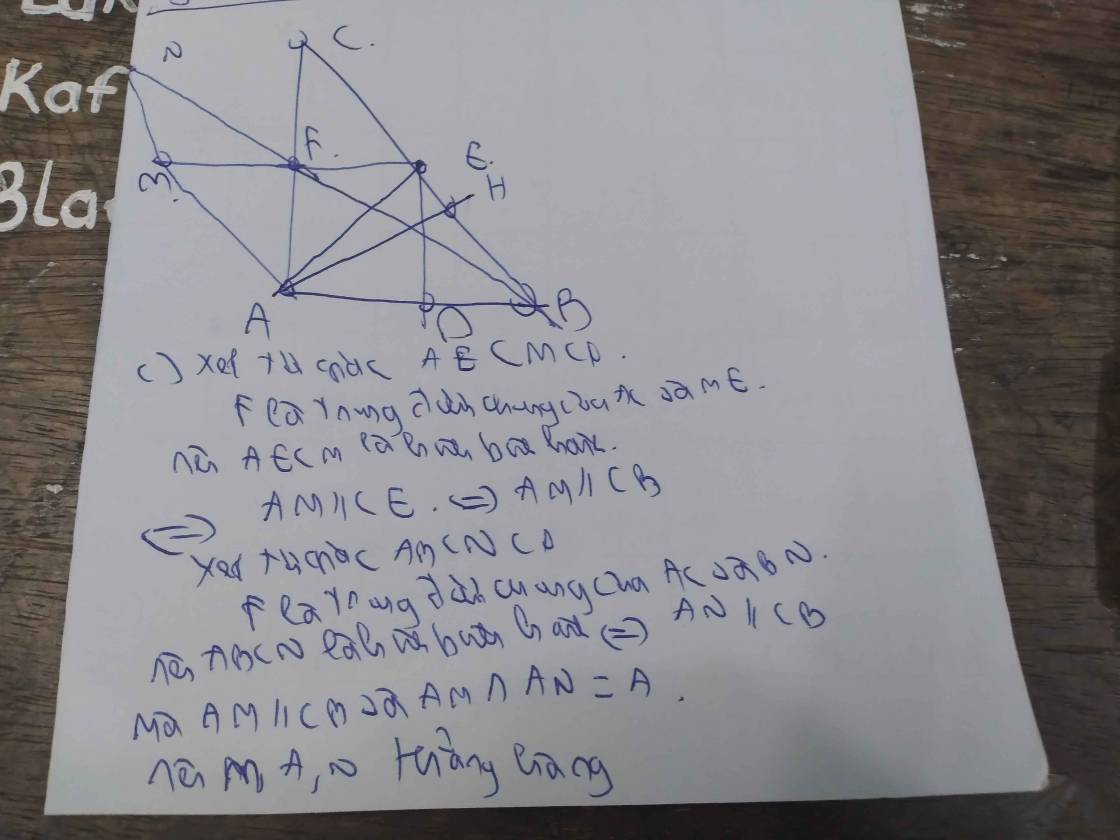
Xét ΔABC có
E là trung điểm của BC
EF//AB
Do đó: F là trung điểm của AC
Xét tứ giác AECM có
F là trung điểm của AC
F là trung điểm của EM
Do đó: AECM là hình bình hành
=>AM//CE
=>AM//CB
Xét tứ giác NMBE có
F là trung điểm chung của NB và ME
=>NMBE là hình bình hành
=>NM//BE
=>NM//BC
AM//BC
NM//BC
mà AM,NM có điểm chung là M
nên M,N,A thẳng hàng
Xét tứ giác
Cảm ơn nha:))