Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé. Tại mình thấy đề AH vuông góc BC hơi sai nên sẽ sửa là EH nha.
Giải
a, Vì EH \(\perp BC\)( gt ) \(\Rightarrow\)\(\Delta HBE\)vuông tại H.
Xét \(\Delta\)vuông ABE và \(\Delta\) vuông HBE, có :
BE : cạnh chung
góc ABE = góc HBE ( BE là tpg góc ABC )
\(\Rightarrow\)\(\Delta\)vuông ABE = \(\Delta\) vuông HBE ( cạnh huyền góc nhọn )
b, Ta có : BA=BH ( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE ) \(\Rightarrow\) \(\Delta BAH\) cân tại B ( đ/n )
Mà góc ABC = 60o ( gt ) \(\Rightarrow\) \(\Delta BAH\) đều.
\(\Rightarrow\)AB=AH=BH ( đ/n )
Xét \(\Delta\) vuông ABC, có :
góc ABC + góc BCA = 90o ( 2 góc phụ nhau )
\(\Rightarrow\)60o + góc BCA = 90o \(\Rightarrow\)góc BCA = 30o
Mà góc EBH = 30o ( vì BE là tpg góc ABC , góc ABC = 60o )
\(\Rightarrow\)góc EBC = góc BCA ( =30o )
\(\Rightarrow\)\(\Delta\)BEC cân tại E ( t/c ) \(\Rightarrow\)BE = EC ( đ/n )
Xét \(\Delta\) vuông HEB và \(\Delta\) vuông HEC , có :
BE=EC ( cmt )
góc EBH = góc ECH ( cmt )
\(\Rightarrow\)\(\Delta\)vuông HEB = \(\Delta\) vuông HEC ( cạnh huyền góc nhọn )
\(\Rightarrow\)BH = CH ( 2 cạnh tương ứng )
c, Xét \(\Delta\) vuông ABE , có :
góc ABE + góc AEB = 90o ( 2 góc phụ nhau ), mà góc ABE = 30o ( BE là tpg góc ABC )
\(\Rightarrow\)góc AEB = 60o
Ta có : góc AEB = góc HEB = 60O( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE )
Mà BE // HK ( gt ) \(\Rightarrow\) góc HEB = góc EHK = 60o( 2 góc so le trong )
Vì BE // HK ( gt ) \(\Rightarrow\) góc AEB = góc EKH = 60o ( 2 góc đồng vị )
Xét \(\Delta EHK\) , có :
góc EHK + góc EKH + góc KEH = 180o ( tổng 3 góc trong tam giác )
\(\Rightarrow\)60o + 60o + góc KEH = 180o
\(\Rightarrow\)góc KEH = 60o
Ta nhận thấy trong tam giác EKH cả 3 góc đều bằng 60o ( cmt )
\(\Rightarrow\)\(\Delta EKH\)là tam giác đều ( t/c)
d, Xét \(\Delta\) AEI và \(\Delta HEC\) , có :
góc EAI = góc EHC ( = 900 )
AE=EH ( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE )
góc AEI = góc HEC ( 2 góc đối đỉnh )
\(\Rightarrow\Delta AEI=\Delta HEC\)( g-c-g )
\(\Rightarrow\)EI = EC ( 2 cạnh tương ứng )
Xét \(\Delta\) vuông HEC, có :
EC > EH ( cạnh huyền > cạnh góc vuông ) , mà EC = EI ( cmt )
\(\Rightarrow\)EI hay IE > EH ( đpcm )

Bạn tự vẽ hình nha.
a,Xét tg ABE và tg HBE:
^BAE=^BHE=90*
^ABE=^HBE(BE là pg)
BE chung
=>tg ABE= tg HBE(ch-gn)
b,+,tg ABC có:^BAC=90*,^ABC=60*
=>^C=30*
+,tg BHE có: ^BHE=90*,^EBH=30*(^EHB=1/2ABC)
=>^HEB=60*
Mà HK // BE
=>^HBE=^EHK=60*(slt)
+, tg CHE có:^EHC=90*,^C=30*
=>HEC=60*
+,tg HEK có:
^EHK=60*,^HEC(^HEK)=60*
=>TG HEK đều(dhnb)
Phần c mik chỉ ghi các bước thôi còn bạn tự chình bày nhé.
c, +,CM:tg AEM=tg HEC(cgv-gnk)
=>AM=HC
+,CM:BM=BC
+,CM:tg BMI=tgBCI(cgc)
=>NM=NC
Xong r nha. Chúc bạn học tốt.

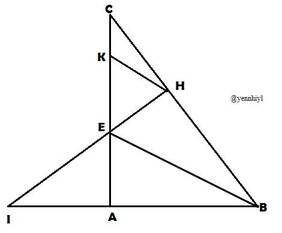
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE

góc ABE=góc HBE=60/2=30 độ
=>góc AEB=góc HEB=60 độ
=>góc AEH=120 độ
HK//BE
=>góc KHE=góc HEB=60 độ
góc KEH=180-120=60 độ
Xét ΔKEH có góc KHE=góc KEH=60 độ
nên ΔKEH đều