Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét tam giác abc vuông tại a
theo đlí pytago có
\(bc=\sqrt{ab^2+ac^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
b,
xét tam giác abm và tam giác bkm có
góc bam=góc bkm(gt)
bm chung
góc abm=góc kbm(gt)
=>tam giác abm = tam giác bkm(gcg)

Giải thích các bước giải:
a)Áp dụng định lí pytago vào tam giác ABC vuông tai A ta có:
AB2+AC2=BC2
=>BC2=62+82
=>BC2=100
=>BC=10 (cm)
b)Xét tam giác ABD vuông tại A và tam giác EBD vuông tai E có:
BD : cạnh chung
góc ABD=góc EBD (BD là p/g của góc ABC)
Suy ra: tam giác ABD= tam giác EBD
c)Ta có AC là đường cao thứ nhất của tam giác BFC
FE là đường cao thứ 2 của tam giác BFC
Mà AC và FE cắt nhau tại D nên D là trực tâm
=>BD là đường cao thứ 3 của tam giác BFC
Mà BD cũng là đường p/g của tam giác BFC nên: tam giác BFC cân ở B
Mà góc FBC=60o(gt)
nên: tam giác FBC đều
d mình đang suy nghĩ do khó quá

a: BC=căn 6^2+8^2=10cm
b: Xét ΔABM vuông tại A và ΔKBM vuông tại K có
BM chung
góc ABM=góc KBM
=>ΔBAM=ΔBKM
c: AM=MK
MK<MC
=>AM<MC
d: Xét ΔMAD vuông tại A và ΔMKC vuông tại K có
MA=MK
góc AMD=góc KMC
=>ΔMAD=ΔMKC
=>AD=KC
Xét ΔBDC có BA/AD=BK/KC
nên AK//DC

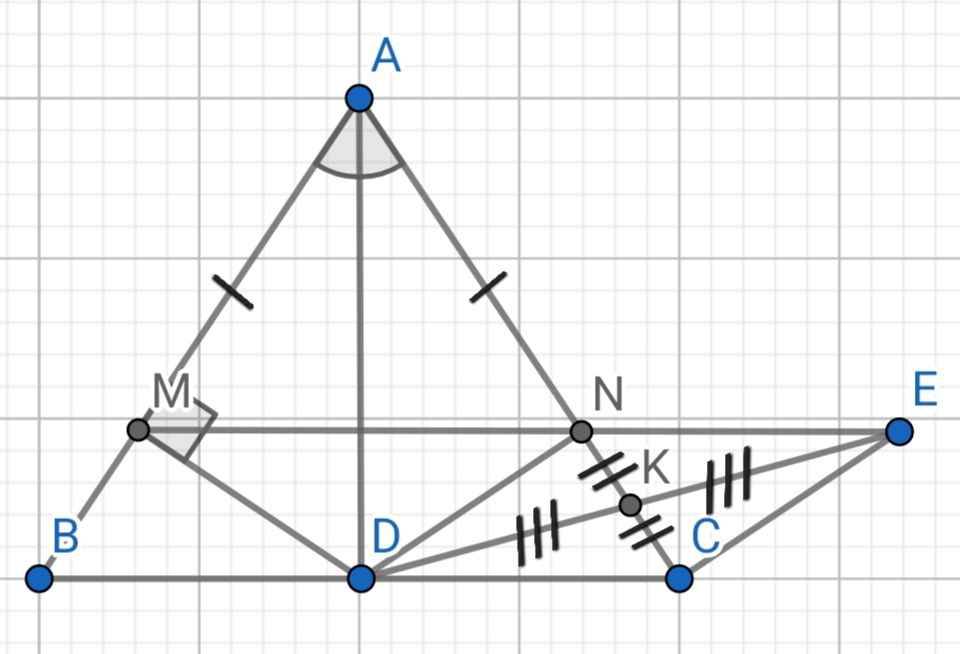 a) Do AD là tia phân giác của ∠BAC (gt)
a) Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠CAD
Do ∆ABC cân tại A
⇒ AB = AC
Xét ∆ABD và ∆ACD có:
AB = AC (cmt)
∠BAD = ∠CAD (cmt)
AD là cạnh chung
⇒ ∆ABD = ∆ACD (c-g-c)
⇒ BD = CD
⇒ D là trung điểm của BC (1)
Do ∆ABD = ∆ACD (cmt)
⇒ ∠ADB = ∠ADC (hai góc tương ứng)
Mà ∠ADB + ∠ADC = 180⁰ (kề bù)
⇒ ∠ADB = ∠ADC = 180⁰ : 2 = 90⁰
⇒ AD ⊥ BC (2)
Từ (1) và (2) ⇒ AD là đường trung trực của BC
b) Sửa đề: Chứng minh ∆ADM = ∆ADN
Do ∠BAD = ∠CAD (cmt)
⇒ ∠MAD = ∠NAD
Xét ∆ADM và ∆ADN có:
AD là cạnh chung
∠MAD = ∠NAD (cmt)
AM = AN (gt)
⇒ ∆ADM = ∆ADN (c-g-c)
⇒ ∠AMD = ∠AND = 90⁰ (hai góc tương ứng)
⇒ DN ⊥ AN
⇒ DN ⊥ AC
d) Do K là trung điểm của CN (gt)
⇒ CK = KN
Xét ∆DKC và ∆EKN có:
CK = KN (cmt)
∠DKC = ∠EKN (đối đỉnh)
KD = KE (gt)
⇒ ∆DKC = ∆EKN (c-g-c)
⇒ ∠KDC = ∠KEN (hai góc tương ứng)
Mà ∠KDC và ∠KEN là hai góc so le trong
⇒ EN // CD
⇒ EN // BC (3)
∆AMN có:
AM = AN (gt)
⇒ ∆AMN cân tại A
⇒ ∠AMN = (180⁰ - ∠MAN) : 2
= (180⁰ - ∠BAC) : 2 (4)
∆ABC cân tại A (gt)
⇒ ∠ABC = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC (6)
Từ (3) và (6) kết hợp với tiên đề Euclide ⇒ M, N, E thẳng hàng

