Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔACI vuông tại C và ΔBHI vuông tại H có
\(\widehat{AIC}=\widehat{BIH}\)(hai góc đối đỉnh)
Do đó: ΔACI~ΔBHI
b: Ta có: ΔCAB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(CB^2=25^2-15^2=400\)
=>\(CB=\sqrt{400}=20\left(cm\right)\)
Xét ΔABC có AI là phân giác
nên \(\dfrac{CI}{CA}=\dfrac{BI}{BA}\)
=>\(\dfrac{CI}{15}=\dfrac{BI}{25}\)
=>\(\dfrac{CI}{3}=\dfrac{BI}{5}\)
mà CI+BI=CB=20cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{CI}{3}=\dfrac{BI}{5}=\dfrac{CI+BI}{3+5}=\dfrac{20}{8}=2,5\)
=>\(CI=2,5\cdot3=7,5\left(cm\right)\)
c: Ta có: ΔACI~ΔBHI
=>\(\widehat{CAI}=\widehat{HBI}\)
mà \(\widehat{CAI}=\widehat{BAH}\)
nên \(\widehat{HBI}=\widehat{HAB}\)
Xét ΔHBI vuông tại H và ΔHAB vuông tại H có
\(\widehat{HBI}=\widehat{HAB}\)
Do đó: ΔHBI~ΔHAB
=>\(\dfrac{HB}{HA}=\dfrac{HI}{HB}\)
=>\(HB^2=HI\cdot HA\)

a, Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A , ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Rightarrow AC^2=25^2-20^2\)
\(\Rightarrow AC^2=225\)
\(\Rightarrow AC=15cm\)
Vậy AC = 15cm .
b,Xét tam giác AMC và tam giác HMB có :
góc MAC = góc MHB = 90độ
góc AMC = góc HMB ( đối đỉnh )
Do đó : tam giác AMC đồng dạng với tam giác HMB ( g.g )
c,Xét tam giác ADB và tam giác AMC có :
góc BAD = góc CAM = 90độ
góc ABD = góc ACM ( vì tam giác AMC đồng dạng với tam giác HMB )
Do đó : tam giác ADB đồng dạng với tam giác AMC ( g.g )
\(\Rightarrow\frac{AC}{AB}=\frac{AM}{AD}\)
\(\Rightarrow AC.AD=AM.AB\)
d, Xét tam giác DBC có BA cắt HC tại M :
\(CH\perp BD\)
\(BA\perp DC\)
\(\Rightarrow\)M là trực tâm của tam giác DBC
Vậy DM vuông góc với BC .
Học tốt

a,Xét tam giác BAC và QEC có:
Góc ABC= Góc CQE
Góc C chung
Góc CQE= Góc CAB ( Vì Góc A + Góc B + Góc C = Góc CQE + Góc C + Góc QEC )
=> BAC đồng dạng với QEC(g-g)(đpcm)
b,
Theo định lý Py-ta-go ta có:
Trong Tam giác ABC vuông tại B
Ta có:
AB^2+BC^2=AC^2
=> AC^2=100
=> AC = 10

a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
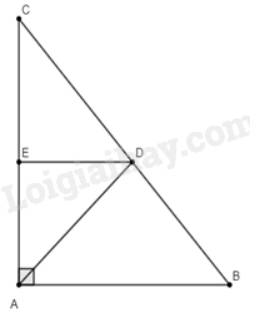
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2

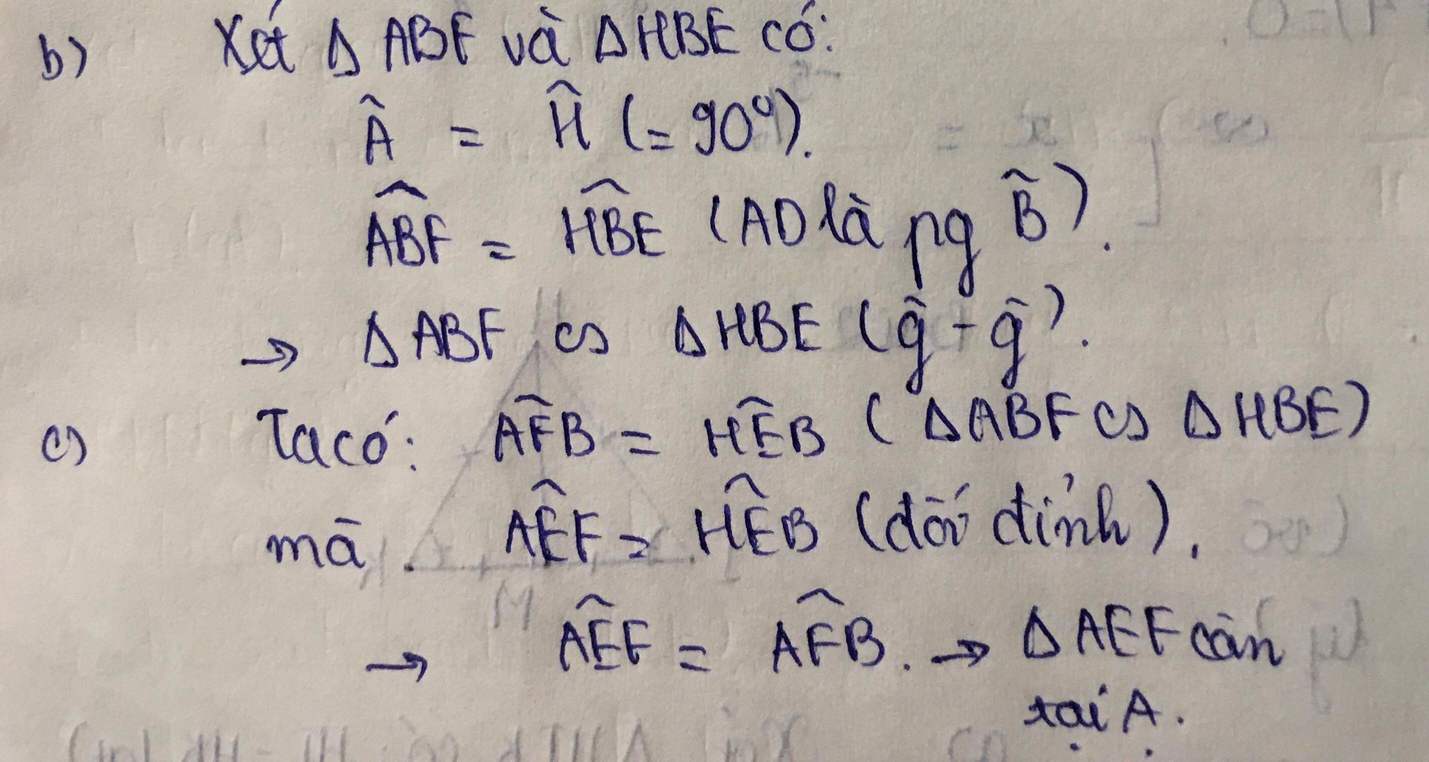
lô