Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc AEH=góc ADH=góc DAE=90 độ
=>ADHE là hình chữ nhật
góc NED=góc NEH+góc DEH
=góc DAH+góc NHE
=góc BAH+góc B=90 độ
=>NE vuông góc ED(1)
góc MDE=góc MDH+góc EDH
=góc MHD+góc EAH
=góc HAC+góc C=90 độ
=>DM vuông góc ED(2)
Từ (1), (2) suy ra ENMD là hình thang vuông
\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BH=6^2/10=3,6cm
=>DM=1,8cm
HC=8^2/10=6,4cm
=>EN=3,2cm
AH=6*8/10=4,8cm
=>ED=4,8cm
\(S_{ENMD}=\dfrac{1}{2}\cdot\left(EN+DM\right)\cdot ED=\dfrac{1}{2}\cdot\left(3,2+1,8\right)\cdot2,4=1,2\cdot5=6\left(cm^2\right)\)

a: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
b: BC=10cm
AH=4,8cm
BH=3,6cm
CH=6,4cm

Vì ADHE là hình chữ nhật nên OD = OH
Suy ra, tam giác ODH cân tại O ⇒ ∠ ODH = ∠ OHD
Mà 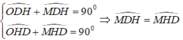
Xét tam giác MBD có:
∠ (MDB) = ∠ (MBD) (vì cùng phụ với hai góc bằng nhau ∠ (MDH) = ∠ (MHD))
Suy ra, tam giác MBD cân tại M, do đó MD = MB (2)
Từ (1) và (2) suy ra, MB = MH
Vậy M là trung điểm của BH
Tương tự, ta cũng có N là trung điểm của CH.

Hình bạn tự vẽ nhé
a, Ta có: D đối xứng với H qua AB \(\Rightarrow\)AB là đường trung trực mà A \(\in\)AB \(\Rightarrow AD=AH\)(1)
Tương tự ta có: \(AH=AE\)(2)
Từ (1), (2) \(\Rightarrow AD=AE\)
\(\Delta ADH\)có: \(AD=AH\left(cmt\right)\Rightarrow\Delta ADH\)cân tại A có AB là đường trung trực \(\Rightarrow\)AB là phân giác của \(\widehat{DAH}\)\(\Rightarrow\widehat{DAB}=\widehat{BAH}\)
Chứng minh tương tự với \(\Delta AHE\)\(\Rightarrow\)AC là phân giác của \(\widehat{HAE}\)\(\Rightarrow\widehat{HAC}=\widehat{CAE}\)
\(\Delta ABC\)có: \(\widehat{BAH}+\widehat{HAC}=90^o\)
Ta có: \(\widehat{DAB}+\widehat{BAH}+\widehat{HAC}+\widehat{CAE}=\widehat{DAE}\)
hay \(2\widehat{BAH}+2\widehat{HAC}=\widehat{DAE}\)
\(2\left(\widehat{BAH}+\widehat{HAC}\right)=\widehat{DAE}\)
\(2.90^o=\widehat{DAE}=180^o\)
\(\Rightarrow\)D, A, E thẳng hàng
mà \(AD=AE\left(cmt\right)\)
\(\Rightarrow\)A là trung điểm của DE
b, Ta có: AB là đường trung trực mà B \(\in\)AB \(\Rightarrow BD=BH\)
Tương tự ta có: \(CH=CE\)
Xét \(\Delta ADB\)và \(\Delta AHB\)có:
AB chung
\(AD=AH\left(cmt\right)\)
\(DB=BH\left(cmt\right)\)
\(\Rightarrow\Delta ADB=\Delta AHB\left(c-c-c\right)\)\(\Rightarrow\widehat{AHB}=\widehat{ADB}=90^o\Rightarrow BD\perp DE\)
Chứng minh tương tự ta có: \(\Delta AHC=\Delta AEC\left(c-c-c\right)\)\(\Rightarrow\widehat{AHC}=\widehat{AEC}=90^o\Rightarrow EC\perp DE\)
Ta có: \(BD\perp DE\left(cmt\right)\)
\(EC\perp DE\left(cmt\right)\)
\(\Rightarrow BD//EC\)
Tứ giác BDEC có: \(BD//EC\left(cmt\right)\)\(\Rightarrow\)BDEC là hình thang có \(\widehat{BDE}=\widehat{DEC}=90^o\Rightarrow\)BDEC là hình thang vuông






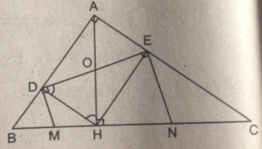
1: Xét ΔACB vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC=4\cdot9=36\)
=>AH=6(cm)
Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>DE=AH=6(cm)
2: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1),(2) suy ra \(AD\cdot AB=AE\cdot AC\)
3: Ta có: ADHE là hình chữ nhật
=>\(\widehat{EDH}=\widehat{EAH};\widehat{AHE}=\widehat{ADE};\widehat{DEH}=\widehat{DAH}\)
\(\widehat{EDM}=\widehat{EDH}+\widehat{MDH}\)
=>\(\widehat{MDH}+\widehat{EAH}=90^0\)
mà \(\widehat{EAH}+\widehat{HCA}=90^0\)(ΔHAC vuông tại H)
nên \(\widehat{MDH}=\widehat{HCA}\)
=>\(\widehat{MDH}=\widehat{MHD}\)
=>MH=MD
Ta có: \(\widehat{MHD}+\widehat{MBD}=90^0\)(ΔHDB vuông tại D)
\(\widehat{MDH}+\widehat{MDB}=\widehat{HDB}=90^0\)
mà \(\widehat{MHD}=\widehat{MDH}\)
nên \(\widehat{MBD}=\widehat{MDB}\)
=>MB=MD
=>MB=MH
=>M là trung điểm của BH
Ta có: \(\widehat{NED}=\widehat{NEH}+\widehat{DEH}\)
=>\(\widehat{NEH}+\widehat{DAH}=90^0\)
mà \(\widehat{DAH}+\widehat{HBA}=90^0\)(ΔHBA vuông tại H)
nên \(\widehat{NEH}=\widehat{NHE}\)
=>NH=NE
Ta có: \(\widehat{NEH}+\widehat{NEC}=\widehat{CEH}=90^0\)
\(\widehat{NHE}+\widehat{NCE}=90^0\)(ΔCEH vuông tại E)
mà \(\widehat{NEH}=\widehat{NHE}\)
nên \(\widehat{NEC}=\widehat{NCE}\)
=>NC=NE
=>NC=NH
=>N là trung điểm của CH