Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C
Gỉa sử \(\Delta ABC\) có \(AB=3AC;\widehat{A}=90^0\)
Khi đó \(S\Delta ABC=\frac{1}{2}.AB.AC=\frac{1}{2}.AB.\frac{1}{3}.AB=24\Rightarrow AB^2=144\Rightarrow AB=12\left(cm\right)\)
\(\Rightarrow AC=4\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+4^2}=4\sqrt{10}\left(cm\right)\)
Gọi cạnh góc vuông nhỏ là x (cm,x>0)
=> cạnh góc vuông lớn là 3x(cm)
Diện tích là 24 \(cm^2\)nên ta có : \(\frac{3x.x}{2}\)= 24 => x=4 (TMĐK)
=> cạnh góc vuông lớn là 12cm
Vậy số đo cạnh huyền là \(4\sqrt{10}\)cm

mk chỉ giải tóm tắt thôi có gì ko hiểu bạn nhắn tin cho mk cùng
https://olm.vn/hoi-dap/detail/57396353599.html
phần c mk cũng chưa làm đc
a, ta có Cos C=\(\frac{CF}{EC}\)
C/m tam giác CEF đồng dạng với tam giác CBA (g-g)
=> \(\frac{CF}{EC}=\frac{AC}{BC}\)
=> tam giác AFC và tam giác BEC dồng dạng (c-g-c)
=>\(\frac{CF}{EC}=\frac{AF}{AE}\)
=> Cos C =\(\frac{AF}{BE}\)=> BE.Cos C= BE.\(\frac{AF}{BE}\)=AF(đpcm)
b,
bn áp dụng các hệ thức về góc và cạnh trong tam giác vuông
mỗi cạnh góc vuông bằng cạnh huyền.Sin góc đối để tính AB,AC trong tam giác ABC vuông
=> AE=EC=AC:2=...(bn tu tinh nha)
xét tam giác CEF vuông tại C
lại áp dụng công thức trên để tính È
=> FC=....(Theo Pi-ta-go)
=>BF=BC-FC
=>BF=....
=>bn tính SABE VÀ SBEF sau đó cộng lại là ra SABFE
- NẾU CÓ BN NÀO GIẢI ĐƯỢC PHẦN C THÌ GIÚP MK VS
- *****CHÚC BẠN HỌC GIỎI*****

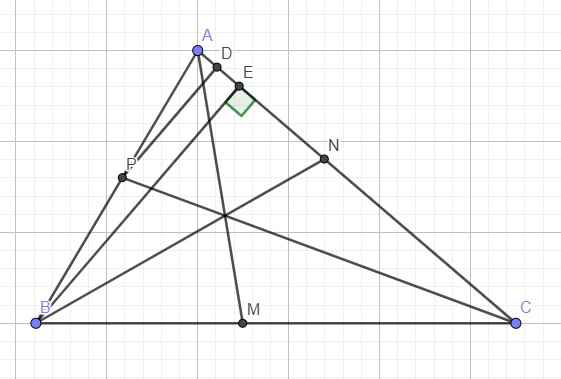
Kẻ PD và BE vuông góc AC
Định lý phân giác: \(\dfrac{AN}{NC}=\dfrac{AB}{BC}\Rightarrow\dfrac{AN}{AN+NC}=\dfrac{AB}{AB+BC}\Rightarrow\dfrac{AN}{AC}=\dfrac{AB}{AB+BC}=\dfrac{c}{a+c}\)
Tương tự: \(\dfrac{AP}{AB}=\dfrac{b}{a+b}\)
Talet: \(\dfrac{PD}{BE}=\dfrac{AP}{AB}\)
\(\dfrac{S_{APN}}{S_{ABC}}=\dfrac{\dfrac{1}{2}PD.AN}{\dfrac{1}{2}BE.AC}=\dfrac{AP}{AB}.\dfrac{AN}{AC}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}\)
Tương tự: \(\dfrac{S_{BPM}}{S_{ABC}}=\dfrac{ac}{\left(a+b\right)\left(b+c\right)}\) ; \(\dfrac{S_{CMN}}{S_{ABC}}=\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{APN}+S_{BPM}+S_{CMN}}{S_{ABC}}=\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\)
\(\Rightarrow\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{S_{ABC}-\left(S_{APN}+S_{BPM}+S_{CMN}\right)}{S_{ABC}}=1-\left(\dfrac{bc}{\left(a+b\right)\left(a+c\right)}+\dfrac{ac}{\left(a+b\right)\left(b+c\right)}+\dfrac{ab}{\left(a+c\right)\left(b+c\right)}\right)\)
\(=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}\)
2. Do ABC cân tại C \(\Rightarrow AC=BC=a\)
\(\dfrac{BC}{AB}=k\Rightarrow AB=\dfrac{BC}{k}=\dfrac{a}{k}\)
Do đó:
\(\dfrac{S_{MNP}}{S_{ABC}}=\dfrac{2abc}{\left(a+b\right)\left(b+c\right)\left(c+a\right)}=\dfrac{2.a.a.\dfrac{a}{k}}{2a.\left(a+\dfrac{a}{k}\right)\left(a+\dfrac{a}{k}\right)}=\dfrac{k}{\left(k+1\right)^2}\)
ta có : a2+b2=289
a.b/2=60
=> a=8
b=15
vậy độ dài hai cạnh góc vuông là 8 và 15