Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mấy bữa nay mình ghét nhất là từ chtt ấy nha câu dễ thì có trong đó nhưng những câu khó tất nhiên ko có rồi mình mong các bạn hỉu ý của mình và ai biết thì làm bài giải đầy đủ sẽ có nhìu người tick chứ cứ chtt hoài mình muốn chết còn sướng hơn các bạn thử nghĩ nếu như một lúc nào đó các bạn có bài giải rất khó nhưng ko biết làm rồi lên đây hỏi mà ai cũng trả lời là chtt các bạn có bực mình ko. Mình chỉ nói thế thôi mong các bạn sẽ hỉu và đừng ghi chữ chtt nữa.

A B C H K O D E F P Q
a) +) Gọi P và Q lần lượt là hình chiếu của O trên các đường thẳng AB và AC.
Tứ giác AHKO là hình chữ nhật => OA // HK hay OA // BC => ^FAO = ^ABC; ^EAO = ^ACB
Mà ^ABC = ^ACB = 450 => ^FAO = ^EAO = 450. Do đó: AO là tia phân giác ^EAF
Xét góc EAF: AO là phân giác ^EAF; OP vuông góc AF; OQ vuông góc AE
=> AP = AQ và OP = OQ (T/c điểm nằm trên đường phân giác)
Xét \(\Delta\)OQE và \(\Delta\)OPF có: ^OQE = ^OPF (=900); OQ = OP; OE = OF
=> \(\Delta\)OQE = \(\Delta\)OPF (Cạnh huyền, cạnh góc vuông) => QE = PF (2 cạnh tương ứng)
Ta có: AQ = AP; QE = PF (cmt) => AQ + QE = AP + PF => AE =AF
Xét \(\Delta\)AEF: ^EAF = 900; AE = AF (cmt) => \(\Delta\)AEF vuông cân tại A (đpcm)
+) Ta thấy \(\Delta\)AEF vuông cân ở A (cmt) => ^AFE = 450 hay ^DFE = 450
Xét (O) có: ^DFE là góc nội tiếp đường tròn (O)
=> \(\widehat{DFE}=\frac{1}{2}.sđ\widebat{DE}\)=> ^DOE = 2.^DFE = 900 => DO vuông góc OE (đpcm).
b) Xét tứ giác DAOE có: ^DAE = ^DOE (=900) => Tứ giác DAOE nội tiếp đường tròn (DE)
hay 4 điểm D;A;O;E cùng nằm trên 1 đường tròn (đpcm).

GIẢI: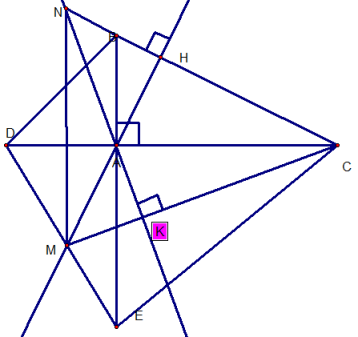
a) Xét Δ ABC và Δ AED, ta có :
(đối đỉnh)
AB = AD (gt)
AC = AD (gt)
=> Δ ABC = Δ AED (hai cạnh góc vuông)
=> BC = DE
Xét Δ ABD, ta có :
(Δ ABC vuông tại A)
=> AD AE
=>
=> Δ ABD vuông tại A.
mà : AB = AD (gt)
=> Δ ABD vuông cân tại A.
=>
cmtt :
=>
mà : ở vị trí so le trong
=> BD // CE
b) Xét Δ MNC, ta có :
NK MC = > NK là đường cao thứ 1.
MH NC = > MH là đường cao thứ 2.
NK cắt MH tại A.
=> A là trực tâm. = > CA là đường cao thứ 3.
=> MN AC tại I.
mà : AB AC
=> MN // AB.
c) Xét Δ AMC, ta có :
(đối đỉnh)
(Δ ABC = Δ AED)
=> (cùng phụ góc ABC)
=> Δ AMC cân tại M
=> AM = ME (1)
Xét Δ AMI và Δ DMI, ta có :
(MN
AC tại I)
IM cạnh chung.
mặt khác : (so le trong)
(đồng vị)
mà : (cmt)
=>
=> Δ AMI = Δ DMI (góc nhọn – cạnh góc vuông)
=> MA = MD (2)
từ (1) và (2), suy ta : MA = ME = MD
ta lại có : ME = MD = DE/2 (D, M, E thẳng hàng)
=>MA = DE/2.