Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Xét ΔEBC vuông tại E và ΔFCB vuông tại F có
BC chung
\(\widehat{ECB}=\widehat{FBC}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEBC=ΔFCB(cạnh huyền-góc nhọn)
Suy ra: \(\widehat{EBC}=\widehat{FCB}\)(hai góc tương ứng)
hay \(\widehat{IBC}=\widehat{ICB}\)
Xét ΔBIC có \(\widehat{IBC}=\widehat{ICB}\)(cmt)
nên ΔIBC cân tại I(Định lí đảo của tam giác cân)
a) Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC(ΔABC cân tại A)
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF(Cạnh huyền-góc nhọn)

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
b: Xét ΔFBC vuông tại F và ΔECB vuông tại E có
FB=EC
FC=EB
BC chung
DO đó: ΔFBC=ΔECB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
hay ΔBIC cân tại I
d: Ta có: AB=AC
nên A nằm trên đường trung trực của BC(1)
Ta có: IB=IC
nên I nằm trên đường trung trực của BC(2)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,M,I thẳng hàng

`#3107.101107`
`a,`
Xét $\triangle ABH$ và $\triangle ACH$:
`AB = AC` $(\triangle ABC$cân tại A`)`
\(\widehat{B}=\widehat{C}\) $(\triangle ABC$cân tại A`)`
`HB = HC ( H` là trung điểm của BC`)`
$=> \triangle ABH = \triangle ACH (c - g - c)$
Vì $\triangle ABH = \triangle ACH$
`=>`\(\widehat{AHB}=\widehat{AHC}\left(\text{2 góc tương ứng}\right)\)
Mà `2` góc này nằm ở vị trí kề bù
`=>` \(\widehat{AHB}+\widehat{AHC}=180^0\)
`=>` \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\) `=> AH \bot BC`
`b,`
Vì $\triangle ABH = \triangle ACH (a)$
`=>`\(\widehat{BAH}=\widehat{CAH}\left(\text{2 góc tương ứng}\right)\)
Xét $\triangle AHM$ và $\triangle AHN$:
AH chung
\(\widehat{MAH}=\widehat{NAH}\left(CMT\right)\)
\(\widehat{AMH}=\widehat{ANH}\left(=90^0\right)\)
$=> \triangle AHM = \triangle AHN (ch - gn)$
`c,`
Xét $\triangle HMB$ và $\triangle HNC$:
\(\widehat{HMB}=\widehat{HNC}\left(=90^0\right)\)
`HB = HC` `(`gt`)`
\(\widehat{HBM}=\widehat{HCN}\) $(\triangle ABC$ cân tại A`)`
$=> \triangle HMB = \triangle HNC (ch - gn)$
`=>`\(\widehat{BHM}=\widehat{CHN}\left(2\text{ góc tương ứng}\right)\) `(1)`
Vì \(\left\{{}\begin{matrix}\widehat{MHB}+\widehat{KHB}=\widehat{MHK}\\\widehat{NHC}+\widehat{IHC}=\widehat{NHI}\end{matrix}\right.\)
Mà \(\widehat{MHK}=\widehat{NHI}\left(\text{đối đỉnh}\right)\) `(2)`
Từ `(1)` và `(2)` `=>` \(\widehat{KHB}=\widehat{IHC}\)
Xét $\triangle KHB$ và $\triangle IHC$:
\(\widehat{KBH}=\widehat{ICH}\left(\widehat{ABC}=\widehat{ACB}\right)\)
`HB = HC`
\(\widehat{KHB}=\widehat{IHC}\)
$=> \triangle KHB = \triangle IHC (g - c - g)$
`=> BK = CI` `(2` cạnh tương ứng`)`
Ta có:
`AK = AB + BK`
`AI = AC + CI`
Mà `AB = AC; BK = CI`
$=> AK = AI => \triangle AIK$ cân tại A.
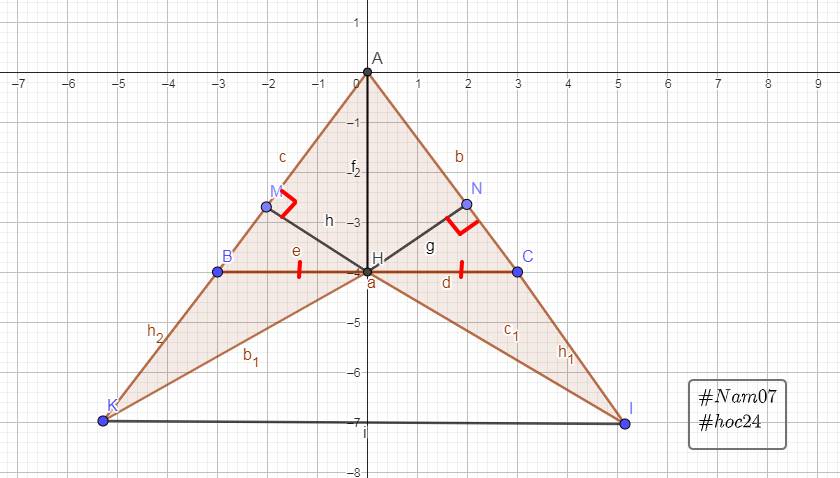

Hình tự vẽ nha bạn
a) Xét \(\Delta AHB\)và \(\Delta AKC\)có:
\(\hept{\begin{cases}\widehat{A}:chung\\AB=AC\left(gt\right)\\\widehat{AHB}=\widehat{AKC}\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta AHB=\Delta AKC\left(ch-gn\right)\)
=>AH=AK ( 2 cạnh tương ứng) -đpcm
b) Xét \(\Delta AKI\)và \(\Delta AHI\)có:
\(\hept{\begin{cases}AK=AH\\\widehat{AKI}=\widehat{AHI}\\AI:chung\end{cases}}\)
\(\Rightarrow\Delta AKI=\Delta AHI\left(ch-cgv\right)\)
\(\Rightarrow\widehat{IAK}=\widehat{IAH}\)( 2 góc tương ứng)
=> AI là ti phân giác góc KAH
Xét \(\Delta KAH\)cân tại A ( do AH=AK ) có AI là tia phân giác ứng cạnh KH
=> AI đồng thời là đường trung trực của cạnh KH (t/c) -đpcm
c) Kẻ CM \(\perp\)BE
Xét tứ giác BKCM có:
\(\hept{\begin{cases}\widehat{CKB}=90^0\\\widehat{KBM}=90^0\\\widehat{BMC}=90^0\end{cases}}\)
=> tứ giác BKCM là hình chữ nhật (dấu hiệu nhận biết)
=> BK=CM (t/c) (1)
Dễ dàng chứng minh đc: BK=CH (2)
Từ (1) và (2) có : CM=CH
Xét \(\Delta BHC\)và \(\Delta BMC\)có:
\(\hept{\begin{cases}CH=CM\\\widehat{BHC}=\widehat{BMC}\\CB:chung\end{cases}}\)
=> \(\Delta BHC=BMC\left(ch-cgv\right)\)
=> \(\widehat{CBH}=\widehat{CBM}\)(2 góc tương ứng)
=> BC là tia phân giác góc HBM
hay BC là tia phân giác HBE -đpcm
Chúc bạn học tốt!
d) Xét tam giác CME vuông tại M có CE là cạnh huyền
=>CE>CM (trong tam giác vuông cạnh huyền là cạnh lớn nhất)
mà CH=CM do \(\Delta CBH=\Delta CBM\)
=>CE>CH

A B D E K C H I
a.Xét hai tam giác vuông ABE và tam giác vuông KBE có
góc ABE = góc KBE = 90độ
cạnh BE chung
góc ABE = góc KBE [ gt ]
Do đó ; tam giác ABE = tam giác KBE [ g.c.g ]
\(\Rightarrow\) AB = KB [ cạnh tương ứng ]
Vậy tam giác ABK cân tại B
b.Xét tam giác ABD và tam giác KBD có
AB = KB [ vì tam giác ABE = tam giác KBE theo câu a ]
góc ABD = góc KBD [ vì BD là tia phân giác góc B ]
cạnh BD chung
Do đó ; tam giác ABD = tam giác KBD [ c.g.c ]
\(\Rightarrow\)góc BAD = góc BKD [ góc tương ứng ]
mà bài cho góc BAD = 90độ nên góc KBD = 90độ
Vậy DK vuông góc với BC
c.Vì DK vuông góc với BC và AH vuông góc với BC nên
DK // AH
Suy ra ; góc HAK = góc DKA [ ở vị trí so le trong ] [ 1 ]
Mặt khác ; AD = DK [ vì tam giác ABD = tam giác KBD ]
\(\Rightarrow\)tam giác ADK là tam giác cân tại D nên
góc DKA = góc DAK [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra
góc HAK = góc DAK
Vậy AK là tia pg góc KAD hay AK là tia pg góc HAC

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
a)vì ABC là tam giác vuông tại A
và AH vuông góc vs BC,dồng thời là đường cao,là đg trung tuyến trong tam giác
nên H=90độ
tam giác AHC vuông tại H
khó quá mà