K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 11 2023
a: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là tia phân giác của \(\widehat{BAC}\) và AD\(\perp\)BC
Xét tứ giác AMEN có
\(\widehat{AME}=\widehat{ANE}=\widehat{MAN}=90^0\)
Do đó: AMEN là hình chữ nhật
Hình chữ nhật AMEN có AE là phân giác của \(\widehat{MAN}\)
nên AMEN là hình vuông
b: AMEN là hình vuông
=>\(\widehat{AMN}=45^0\)
=>\(\widehat{AMN}=\widehat{ABC}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí đồng vị
nên MN//BC
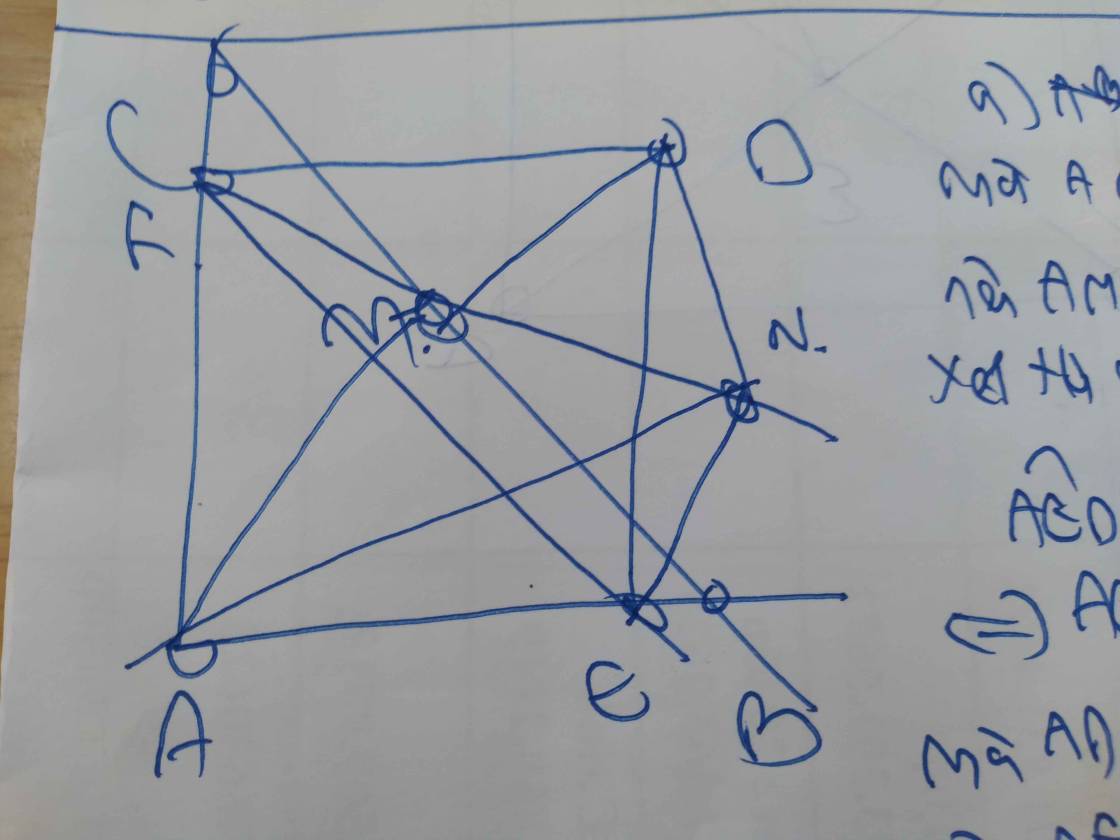
xét tam giác vuông ABN và tam giác vuông ACM
có: AB=AC (gt)
AN=AM gt)
=>tam giác ABN=tam giác ACM (2 cạnh góc vuông)
=>BN=CM (2 cạnh tương ứng) (1)
Gọi K là giao điểm của FM và CA
ta có : góc FMB + góc MBN=900
góc KMA + góc MAK = 900
Mà góc KMA = góc BMF (đối đỉnh)
=>góc MBN= góc MKA
xét tam giác vuông MAK và tam giác vuông NAB
có :AM =AN (gt)
góc MBN= góc MKA (cmt)
=> tam giác MAK = tam giác NAB (cạnh góc vuông góc nhọn)
=>AK =AB ( 2 cạnh tương ứng ) (2)
từ (1) và (2) =>AK =AC
ta có KM vuông góc với BN
=>KF vuông góc với BN
Mà AE vuông góc với BN (gt)
=>KF //AE
Ta có AK =AC (cmt)
=>AE là đường trung bình của tam giác KFC
=>È = EC
hay E là trung điểm của FC