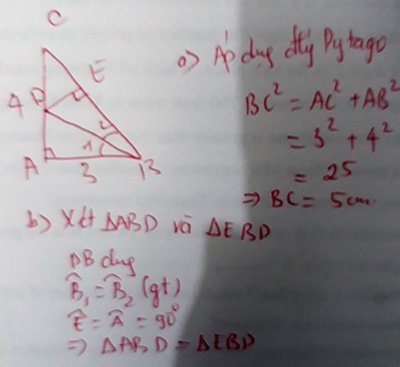Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Vậy: BC=5cm
Xét ΔABD vuông tại A
ΔEBD vuông tại E
CÓ : BD : CẠNH HUYỀN CHUNG
\(\widehat{ABD}=\widehat{EBD}\) (D LÀ TIA PHÂN GIÁC CỦA GÓC B)
⇒ΔABD= ΔEBD (CẠNH HUYỀN-CẠNH GÓC VUÔNG)
C)XÉT ΔDAI VUÔNG TẠI A
ΔDEC VUÔNG TẠI E
CÓ: \(\widehat{A}=\widehat{E}\)(GT)
AD=CD(ΔABD= ΔEBD)
\(\widehat{ADI}=\widehat{EDC}\) (ĐỐI ĐỈNH)
⇒ΔDAI=ΔDEC (G-C-G)
⇒DI = CD
⇒ΔIDC CÂN TẠI D

bạn tự vẽ hình nha
a) Áp dụng định lý Pi-ta-go cho tam giác ABC vuông tại A
=> \(AB^2+AC^2=BC^2\)
\(3^2+4^2=BC^2\)
\(9+16=BC^2\)
=> \(BC^2=25\)
=>\(BC=5\)
b) Xét tam giác ABD và tam giác EBD có:
\(\widehat{BAD}=\widehat{BED}\left(=90độ\right)\)
BD chung
\(\widehat{ABD}=\widehat{EBD}\left(gt\right)\)
=> tam giác ABD = tam giác EBD (ch-gn)
c)Vì tam giác ABD = tam giác EBD
=>\(BA=BE\left(1\right)\)
Theo đề bài ta có:
\(AK=EC\left(2\right)\)
Cộng 2 vế của (1),(2)
=>\(BA+AK=BE+EC\)
\(BK=BE\)
=> tam giác BKC cân
=>\(\widehat{BKC}=\widehat{BCK}\)
d)Xét tam giác BAI và tam giác BEI có:
IB chung
\(\widehat{ABI}=\widehat{EBI}\left(gt\right)\)
\(AB=BE\)
=> tam giác BAI = tam giác BEI (c-g-c)
=>AI = EI

a, Xét ∆ ABC vuông tại A
➡️AB2 + AC2 = BC2 (Pitago)
➡️BC2 = 32 + 42
➡️BC2 = 25
➡️BC = 5 (cm)
b, Xét ∆ ABD và ∆ EBD có:
Góc A = góc E = 90°
BD chung
Góc ABD = góc EBD (gt)
➡️∆ ABD = ∆ EBD (ch - gn)
➡️AB = EB (2 cạnh t/ư)
c, Ta có:
BA + AK = BK
BE + EC = BC
mà AB = EB (cmt)
AK = EC (gt)
➡️BK = BC
Xét ∆ BKI và ∆ BCI có:
BK = BC (cmt)
Góc ABD = góc EBD (gt)
BI chung
➡️∆ BKI = ∆ BCI (c.g.c)
➡️Góc BKI = góc BCI (2 góc t/ư)
d, Xét ∆ ABI và ∆ EBI có:
AB = EB (cmt)
Góc ABD = góc EBD (gt)
BI chung
➡️∆ ABI = ∆ EBI (c.g.c)
➡️IA = IE (2 cạnh t/ư)
Hok tốt~

a, xet tam giac ADB va tam giac EBD co:
goc ABD = goc EBD (vi BD la tia phan giac cua goc B)
BD chung
goc BAD = goc BED (=90 do)
suy ra tam giac ADB = tam giac EBD
b,vi tam giac ABC la tam giac vuong nen theo dinh ly pi-ta-go ta co:
BC^2 = AB ^2 + AC^2
= 6^2 + 8^2
= 36+64
=100 suy ra BC = 10
ta co tam giac ABC = tam giac EBD nen AB = BE = 6
ta co EC = BC - BE
= 10 - 6
=4
c,d ban tu lm

a)Ta có: BC2=52=25 (1)
AB2+AC2=32+42=25 (2)
Từ (1);(2)=>BC2=AB2+AC2(=25)
=>tam giác ABC vuông tại A (PyTaGo đảo)
b)Xét tam giác ABD vuông ở A và tam giác EBD vuông ở E(vì DE _|_ BC) có:
BD:cạnh chung
^ABD=^EBD (vì BD là phân giác của ^ABE)
=>tam giác ABD=tam giác EBD(ch-gn)
=>DA=DE (cặp cạnh t.ứ)
b)Xét tam giác ADF có: DF>DA (cạnh huyền>cạnh góc vuông)
Mà DA=DE(cmt)
=>DF>DE
Xét tam giác ADF vuông ở A và tam giác EDC vuông ở E có:
DA=DE(cmt)
^ADF=^EDC (2 góc đối đỉnh)
=>tam giác ADF=tam giác EDC (cgv-gnk)
=>DF=DC (cặp cạnh t.ứ)
DF ko bằng DE bn nhé!

A) Xét ΔABD và ΔEBD có:
+) AB=BE (gt)
+) góc ABD= góc EBD (do BD là phân giác góc B)
+) BD chung
=> ΔABD = ΔEBD (c-g-c)
b)
Qua C kẻ đường thẳng vuông góc với BD tại H.
Xét ΔBCF có: BH là đường cao đồng thời là phân giác của góc B
=> ΔBCF cân tại B (tính chất)
=> BC= BF (điều phải chứng minh)
c)
Xét ΔABC và ΔEBF có:
+) AB = EB (gt)
+) góc B chung
+) BC= BF (câu b)
=> ΔABC = ΔEBF (c-g-c)
d)
Từ ý a, ΔABD = ΔEBD (c-g-c)
=> góc BAD= góc BED = 90
=> DE ⊥ BC
Xét ΔBCF có: BH và CA là 2 đường cao cắt nhau tại D
=> D là trực tâm
=> FD ⊥ BC
=> DE trùng với FD
=> D,E,F thẳng hàng

a: BC=căn 4^2+3^2=5cm
AC<AB<BC
=>góc B<góc C<góc A
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
c: Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
góc EBF chung
=>ΔBEF đồng dạng với ΔBAC
=>BF=BC

Bạn tự vẽ hình nha![]()
a.
Tam giác ABC vuông tại A có:
\(BC^2=AB^2+AC^2\) (định lý Pytago)
\(BC^2=6^2+8^2\)
\(BC^2=36+64\)
\(BC^2=100\)
\(BC=\sqrt{100}\)
\(BC=10\)
b.
Xét tam giác ABD vuông tại A và tam giác HBD vuông tại H có:
BD là cạnh chung
ABD = HBD (BD là cạnh chung của ABH)
=> Tam giác ABD = Tam giác HBD (cạnh huyền - góc nhọn)
=> AD = HD (2 cạnh tương ứng)
c.
Xét tam giác ADK và tam giác HDC có:
KAD = CHD ( = 90 )
AD = HD (theo câu b)
ADK = HDC (2 góc đối đỉnh)
=> Tam giác ADK = Tam giác HDC (g.c.g)
=> KD = CD (2 cạnh tương ứng)
=> Tam giác DKC cân tại D
d.
Tam giác HDC vuông tại H có:
DC > DH (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà DH = DA (theo câu b)
=> DC > DA
Chúc bạn học tốt![]()
a)Ta có tam giac ABC vuông tại A ,áp dụng định lý Ta-lét ta có:BC2=AB2+AC2<=>BC2=82+62<=>BC=10
b)Ta có :BD là phân giác =>B1=B2;DH vuông góc với BC=>H1=H2=90O.Xét tam giác BAD vàBHD:
B1=B2;BD chung;A=H1=90O=>tam giác BAD=BHD=>DA=DH
c)S ở đâu
d)Ta có trong tam giác vuông DHC :DC>DH,HC ;mà DH=DA=>DC>DA
B A C 6 cm 8 cm D H 1 2 1 2