Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

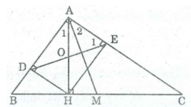
Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông).
+ Xét ∆ ADH và ∆ EHD có :
DH chung
AD = EH ( vì ADHE là hình chữ nhật)
∠ (ADN) = ∠ (EHD) = 90 0
Suy ra: ∆ ADH = ∆ EHD (c.g.c)
⇒ ∠ A 1 = ∠ (HED)
Lại có: ∠ (HED) + ∠ E 1 = ∠ (HEA) = 90 0
Suy ra: ∠ E 1 + ∠ A 1 = 90 0
∠ A 1 = ∠ A 2 (chứng minh trên) ⇒ ∠ E 1 + ∠ A 2 = 90 0
Gọi I là giao điểm của AM và DE.
Trong ∆ AIE ta có: ∠ (AIE) = 180o – ( ∠ E 1 + ∠ A 2 ) = 180 0 - 90 0 = 90 0
Vậy AM ⊥ DE.

a, Vì \(\widehat{AEH}=\widehat{ADH}=\widehat{DAE}=90^0\) nên AEHD là hcn
Do đó AH=DE
b, Vì \(\widehat{HAB}=\widehat{MCA}\) (cùng phụ \(\widehat{CAH}\))
Mà \(\widehat{MCA}=\widehat{MAC}\) (do \(AM=CM=\dfrac{1}{2}BC\) theo tc trung tuyến ứng ch)
Vậy \(\widehat{HAB}=\widehat{MAC}\)
c, Gọi O là giao AM và DE
Vì AEHD là hcn nên \(\widehat{HAB}=\widehat{ADE}\Rightarrow\widehat{MAC}=\widehat{ADE}\)
Mà \(\widehat{ADE}+\widehat{AED}=90^0\left(\Delta AED\perp A\right)\) nên \(\widehat{MAC}+\widehat{ADE}=90^0\)
Xét tam giác AOE có \(\widehat{AOE}=180^0-\left(\widehat{MAC}+\widehat{ADE}\right)=90^0\)
Vậy AM⊥DE tại O
Bạn xem bài làm ở đây:
Câu hỏi của Nguyễn Desmond - Toán lớp 8 - Học toán với OnlineMath