Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

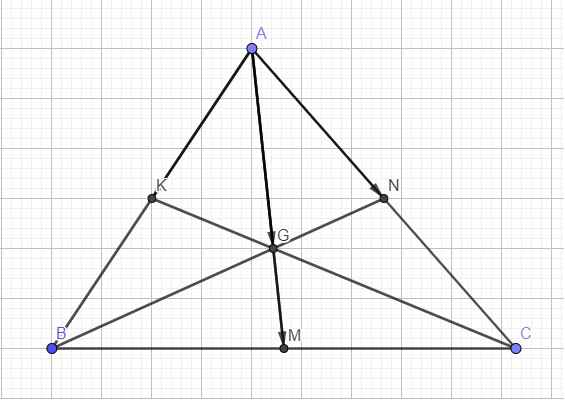
Theo tính chất trọng tâm ta có: \(\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)
Mặt khác AM là trung tuyến nên: \(\overrightarrow{AM}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\right)\Rightarrow3\overrightarrow{AG}=\overrightarrow{AB}+\overrightarrow{AC}\) (1)
K là trung điểm AB, N là trung điểm AC nên: \(\left\{{}\begin{matrix}\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}\\\overrightarrow{AN}=\dfrac{1}{2}\overrightarrow{AC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=2\overrightarrow{AK}\\\overrightarrow{AC}=2\overrightarrow{AN}\end{matrix}\right.\) (2)
(1);(2) \(\Rightarrow3\overrightarrow{AG}=2\left(\overrightarrow{AK}+\overrightarrow{AN}\right)\)

Do BN là trung tuyến
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\\\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{BC}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}\\2\overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{BC}\end{matrix}\right.\)
Cộng vế với vế:
\(\overrightarrow{AM}+2\overrightarrow{BN}=\dfrac{3}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{AM}+\dfrac{4}{3}\overrightarrow{BN}\)

Mình không biết trả lời.Mình mới học lớp 5 thôi .Mong bạn thông cảm nhé!
hình : A B C M P N I
bài làm :
ta có : \(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\)
\(=\overrightarrow{AI}+\overrightarrow{IM}+\overrightarrow{BI}+\overrightarrow{IN}+\overrightarrow{CI}+\overrightarrow{IP}\)
\(=\left(\overrightarrow{AI}+\overrightarrow{IN}\right)+\left(\overrightarrow{BI}+\overrightarrow{IP}\right)+\left(\overrightarrow{CI}+\overrightarrow{IM}\right)\)
\(=\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}\) \(=\overrightarrow{AN}+\overrightarrow{CM}+\overrightarrow{BP}\)
\(=\overrightarrow{NC}+\overrightarrow{CM}+\overrightarrow{BP}=\overrightarrow{NM}+\overrightarrow{BP}=\overrightarrow{PB}+\overrightarrow{BP}=\overrightarrow{PP}=\overrightarrow{0}\left(đpcm\right)\)