Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có ˆM1+ˆM2=180∘M1^+M2^=180∘ nên chỉ có hai khả năng xảy ra ứng với các vị trí của M trên BC là ˆM1>90∘M1^>90∘ hoặc ˆM2≥90∘M2^≥90∘.
– Nếu ˆM1>90∘M1^>90∘ thì tam giác AMC có góc tù nên AM > AC
– Nếu ˆM2≥90∘M2^≥90∘ thì trong tam giác ABM có AM < AB. Kết hợp với giả thiết AB < AC, ta suy ra AM < AC. Vậy ta luôn có AM < AC.

A B C M I H N
- Hạ \(BI\perp AC\)và \(MH\perp AC\)
Xét \(\Delta BIC\)và \(\Delta MHN\)có:
\(HN< IC\)
\(HM< BI\)
\(MN^2=HN^2+HM^2\)
\(BC^2=BI^2+IC^2\)
\(\Rightarrow MN< BC\)
Mà \(BC< AC\Rightarrow MN< BC\)
Cách 2: Xét \(\Delta MHN\)và \(\Delta MHC\)có:
MH chung
HN<HC
\(\hept{\begin{cases}MN^2=MH^2+HN^2\\MC^2=MH^2+HC^2\end{cases}\left\{MN< MC\right\}}\)
Mà MC<BC<AC => MN<AC

Giải
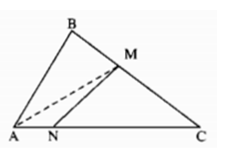
Kẻ đoạn thẳng AM. Xét tam giác MAC. Chứng minh tương tự như bài 1.4 ta có MN < a, trong đó a là đoạn lớn nhất trong hai đoạn thẳng MA và MC. Nếu ta chứng minh được
MA < AC và MC < AC thì sẽ suy ra được a < AC, từ đó có MN < AC.
Trong tam giác ABC có AB ≤ AC, M ∈ BC (M ≠ B, M ≠ C); Chứng minh tương tự bài 1.4, ta có AM < AC. Mặt khác MC < BC ≤ CA. Vậy a < AC, suy ra MN < AC.
bạn ơi cách này trong phần giải đằng sau sách bài tập toán 7 mà !!!

B A C M N
Áp dụng bất đẳng thức tam giác cho tam giác CMN ta có:
\(CN+CM>MN\)
Vì N nằm trên BC nên CN<BC
Vì M nằm trên AC nên CM<AC
=>\(BC+AC>CM+CN>MN\)
Đến đây tự giải tiếp thì dễ rồi