Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nhé!
a, Có ∠BAH+ ∠BAD+ ∠DAM= 180 độ
=> ∠BAH+ ∠DAM= 180 độ- ∠BAD= 90 độ
Xét ΔDAM và ΔABH có
∠ DMA= ∠AHB = 90 độ
AD= AB
∠DAM= ∠ABH (vì cùng phụ với ∠BAH)
=> ΔDAM = ΔABH (ch-gn)
=> DM= AH
b, Có ∠HAC+ ∠EAC+ ∠NAE= 180 độ
=> ∠HAC+ ∠NAE= 180 độ- ∠EAC= 90 độ
Xét ΔEAN và ΔACH có
∠ ANE= ∠AHC = 90 độ
AE= AC
∠NAE= ∠ACH (vì cùng phụ với ∠HAC)
=> ΔEAN = ΔACH (ch-gn)
=> EN= AH
Mà DM= AH
=> EN= DM
c, Có EN ⊥ AH
DM ⊥ AH
=> EN // DM
=> ∠NEO= ∠ODM (2 góc so le trong)
Xét ΔDOM và ΔEON có
∠DMO = ∠ENO = 90 độ
DM= EN
∠ODM= ∠OEN(cmt)
=> ΔDOM = ΔEON (ch-gn)
=> OD = OD
=> O là trung điểm của DE

 a) Ta có :
a) Ta có :
Góc A2 + A3 + A1 = 189' ( bù nhau )
mà góc A3 = 90'
---> góc A2 + góc A1 = 180 - 90' = 90'
Vì góc DMA = góc AHB = 90'
--->góc D2 + góc A2 = 190' - góc DMA
--->góc D2 + góc A2 = 90'
---> góc A1 + góc B1 = 90'
--->góc D1 = góc A1; góc A2 = góc B1
xét hai tam giác vuông AMD và AHB có :
góc DMA = góc AHB ( vuông góc )
AD = AB ( GT )
góc A2 = góc B1 ( CMT )\
--->ΔDMA = ΔAHB ( cạnh huyền - góc nhọn )
---> DM = AH ( hai cạnh tương ứng)
b) Gọi M là giao điểm của MN và DE
Xét ΔANE và ΔCHA có :
( chứng minh như câu a)
---> EN = AH
Xét hai tam giác vuông IEN và IMD có :
góc I1 = góc I2 ( đối đỉnh )
EN = AH ( ΔANE = ΔCHA)
DM = AH ( CMT )
vì Tổng 3 góc tam giác = 180'
mà góc I1 = góc I2 ;
Góc M = góc N
---> ΔIMD = ΔENI ( cạnh huyền - góc nhọn)
---> DI = IE ( hai cạnh tương ứng 0
---> MN đi qua trung điểm của DE

Ta có: ∠(HAC) +∠(CAE) +∠(EAN) =180o(kề bù)
Mà ∠(CAE) =90o⇒∠(HAC) +∠(EAN) =90o (4)
Trong tam giác vuông AHC, ta có:
∠(AHC) =90o⇒∠(HAC) +∠(HCA) =90o (5)
Từ (4) và (5) suy ra: ∠(HCA) =∠(EAN) ̂
Xét hai tam giác vuông AHC và ENA, ta có:
∠(AHC) =∠(ENA) =90o
AC = AE (gt)
∠(HCA) =∠(EAN) ( chứng minh trên)
Suy ra : ΔAHC= ΔENA(cạnh huyền, góc nhọn)
Vậy AH = EN (hai cạnh tương ứng)
Từ (3) và (6) suy ra: DM = EN
Vì DM ⊥ AH và EN ⊥ AH (giả thiết) nên DM // EN (hai đường thẳng cùng vuông góc với đường thẳng thứ ba)
Gọi O là giao điểm của MN và DE
Xét hai tam giác vuông DMO và ENO, ta có:
∠(DMO) =∠(ENO) =90o
DM= EN (chứng minh trên)
∠(MDO) =∠(NEO)(so le trong)
Suy ra : ΔDMO= ΔENO(g.c.g)
Do đó: DO = OE ( hai cạnh tương ứng).
Vậy MN đi qua trung điểm của DE
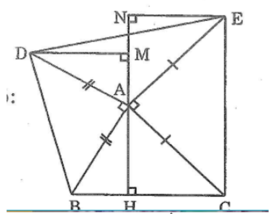

Do tam giác ABD vuông cân tại A => góc DAM + góc BAH = 90º. Trong tam giác vuông ABH có góc ABH + góc BAH = 90º => góc DAM = góc ABH (cùng phụ với một góc bằng nhau)
Xét tam giác vuông ADM và tam giác vuông BAH có:
AD = AB (gt)
góc DAM = góc ABH (cmt)
=> tam giác ADM = tam giác BAH (cạnh huyền - góc nhọn)
=> DM = AH
Cmtt ta có: tam giác ANE = tam giác CHA => EN = AH
=> DM = EN (cùng bằng AH)
Lại có: DM // EN (cùng _|_ AH) mà DM = EN (cmt) => tứ giác DMEN là hình bình hành => MN cắt DE tại trung điểm mỗi đường hay MN đi qua trung điểm của DE.

Bạn vẽ hình ra nhé!
Do tam giác ABD vuông cân tại A => góc DAM + góc BAH = 90º. Trong tam giác vuông ABH có góc ABH + góc BAH = 90º => góc DAM = góc ABH (cùng phụ với một góc bằng nhau)
Xét tam giác vuông ADM và tam giác vuông BAH có:
AD = AB (gt)
góc DAM = góc ABH (cmt)
=> tam giác ADM = tam giác BAH (cạnh huyền - góc nhọn)
=> DM = AH
Cmtt ta có: tam giác ANE = tam giác CHA => EN = AH
=> DM = EN (cùng bằng AH)
Lại có: DM // EN (cùng _|_ AH) mà DM = EN (cmt) => tứ giác DMEN là hình bình hành => MN cắt DE tại trung điểm mỗi đường hay MN đi qua trung điểm của DE.
Chúc bạn học giỏi!
tk mk nha bạn
thank you bạn
(^_^)

A B C H D M N E I
Giải:
a, Ta có: \(\widehat{ABH}+\widehat{BAH}=90^o\left(\widehat{AHB}=90^o\right)\)
\(\widehat{MAD}+\widehat{BAH}=90^o\left(\widehat{DAB}=90^o\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{MAD}\)
Xét \(\Delta ABH,\Delta DAM\) có:
AB = AD ( gt )
\(\widehat{AHB}=\widehat{DMA}=90^o\)
\(\widehat{ABH}=\widehat{MAD}\) ( cmt )
\(\Rightarrow\Delta ABH=\Delta DAM\) ( c.huyền - g.nhọn )
\(\Rightarrow AH=DM\) ( cạnh t/ứng ) ( đpcm )
b, Gọi I là giao của DE và MN
Chứng minh tương tự phần a ta có NE = AH ( đpcm )
\(\Rightarrow DM=NE\)
Có: \(\widehat{IDM}+\widehat{DIM}=90^o\left(\widehat{DMI}=90^o\right)\)
\(\widehat{NEI}+\widehat{EIN}=90^o\left(\widehat{ENI}=90^o\right)\)
Mà \(\widehat{DIM}=\widehat{EIN}\) ( đối đỉnh )
\(\Rightarrow\widehat{IDM}=\widehat{NEI}\)
Xét \(\Delta DMI,\Delta ENI\) có:
\(\widehat{IDM}=\widehat{IEN}\left(cmt\right)\)
DM = NE ( cmt )
\(\widehat{DMI}=\widehat{ENI}\left(=90^o\right)\)
\(\Rightarrow\Delta DMI=\Delta ENI\left(g-c-g\right)\)
\(\Rightarrow DI=IE\) ( cạnh t/ứng )
\(\Rightarrow\)I là trung điểm của DE
\(I\in MN\Rightarrow MN\) đi qua trung điểm của DE
A B C E D M N H F
a, Do tam giác ABH vuông tại H => \(\widehat{ABH}+\widehat{BAH}=90^0\) (1)
Mà \(\widehat{BAH}+90^0+\widehat{DAM}=180^0\Rightarrow\widehat{BAH}=\widehat{DAM}=90^0\) (2)
Từ (1) và (2) => \(\widehat{ABH}=\widehat{DAM}\)
Xét \(\Delta BAH\) và \(\Delta ADM\) có:
\(\widehat{DMA}=\widehat{AHB}=90^0\)
AB=AD (gt)
\(\widehat{ABH}=\widehat{DAM}\) (cmt)
\(\Rightarrow\Delta BAH=\Delta ADM\left(CH-GN\right)\)
=> DM=AH (2 cạnh tương ứng)
Vậy DM=AH.
b, Vì tam giác AHC vuông tại H \(\Rightarrow\widehat{HAC}+\widehat{HCA}=90^0\) (3)
Mà \(\widehat{HAC}+90^0+\widehat{NAE}=180^0\Rightarrow\widehat{HAC}+\widehat{NAE}=90^0\) (4)
Từ (3) và (4) \(\Rightarrow\widehat{HCA}=\widehat{NAE}\)
Xét tam giác AHC và tam giác ENA có:
\(\widehat{AHC}=\widehat{ENA}=90^0\)
AC=AE (gt)
\(\widehat{HCA}=\widehat{NAE}\) (cmt)
\(\Rightarrow\Delta AHC=\Delta ENA\left(CH-GN\right)\Rightarrow AH=EN\)
Mà AH=DM (cmt) => DM=EN
Gọi F là giao điểm của NM và DE, xét \(\Delta DFM\) và \(\Delta EFN\) có:
\(\widehat{DFM}=\widehat{EFN}\left(đ^2\right)\)
DM=EN
\(\widehat{DMF}=\widehat{ENF}=90^0\)
=> \(\Delta DFM=\Delta EFN\left(CH-GN\right)\) => DF=EF. Mặt khác, F thuộc DE => F là trung điểm của DE => MN đi qua trung điểm của DE (F thuộc MN)
Vậy MN đi qua trung điểm của DE