Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B A C K E I M G
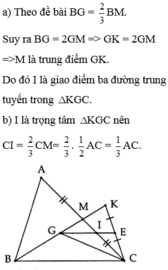
a) Ta có:MK=GK-GM=BG-1/2BG=1/2BG=1/2GK=>M là trung điểm GK
Xét \(\Delta\)KGC có 2 đường trung tuyến là CM và GE cắt nhau tại I
=> I là trọng tâm của \(\Delta\)KGC
b)Do I là trọng tâm của \(\Delta\)KGC
Nên: CI=2/3MC
Mà: MC=1/2AC
Suy ra: CI=1/3AC

a) Ta có : MK = GK - GM = BG - 1/2 BG = 1/2BG = 1/2GK
=> M là trung điểm GK
Ta thấy tam giác KGC có 2 dg trung tuyến CM và GE cắt nhau tại I
=> I là trọng tâm tam giác KGC
b) Do I là trọng tâm tam giác KGC nên CI = 2/3MC
Mà MC = 1/2AC
=> CI = 1/3AC

Vì GM = 1/2 GB (gt)
Mà GB = GD ( G là trung điểm của BD ) nên GM = 1/2 GD
Và M là trung điểm của GD nên CM là đường trung tuyến
Ta có 2 trung tuyến CM và GE cắt nhau tại I nên I là trọng tâm của tam giác CGD