Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

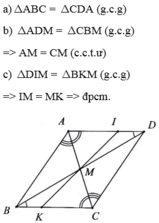
A B C M D I K
a) Do AD // BC (gt) => góc DAC = góc ACB (so le trong)
AB // CD (gt) => góc BAC = góc ACD (so le trong)
Xét t/giác ABC và t/giác CDA
có góc ACB = góc DAC (cmt)
AC : chung
góc BAC = góc ACD (cmt)
=> t/giác ABC = t/giác CDA (g.c.g)
b) Ta có : t/giác ABC = t/giác CDA (cmt)
=> AB = CD (hai cạnh tương ứng)
Do AB // CD (gt) => góc ABD = góc BDC (so le trong)
Xét t/giác AMB và t/giác CMD
có góc BAM = góc MCD (cmt)
AB = CD (cmt)
góc ABM = góc BDM (cmt)
=> t/giác AMB = t/giác CMD (g.c.g)
=> AM = MC (hai cạnh tương ứng)
=> M là trung điểm của AC
c) Xét t/giác AMI và t/giác CMK
có góc DAC = góc ACK (cmt)
AM = CM (cmt)
góc IMA = góc CMK (đối đỉnh)
=> t/giác AMI = t/giác CMK (g.c.g)
=> MI = MK (hai cạnh tương ứng)
=> M là trung điểm của IK
Kuroba Kaito, mình đã biết I, M, K có thẳng hàng đâu. mới chứng minh được MI=Mk nên chưa thể nói M là trung điểm của IK được

a: Xét ΔABC và ΔCDA có
\(\widehat{ACB}=\widehat{CAD}\)
AC chung
\(\widehat{CAB}=\widehat{ACD}\)
Do đó: ΔABC=ΔCDA
b: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
Suy ra: Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
hay M là trung điểm của AC
c: Xét ΔAMI và ΔCMK có
\(\widehat{IAM}=\widehat{KCM}\)
AM=CM
\(\widehat{AMI}=\widehat{CMK}\)
Do đó: ΔAMI=ΔCMK
Suy ra: MI=MK
mà M,I,K thẳng hàng
nên M là trung điểm của IK

Bài làm
a) xét tam giác AED và tam giác MDE có:
^ADE = ^DEM ( do AD // EM )
ED chung
^EDM = ^AED ( do AE // DM )
=> Tam giác AED = tam giác MDE ( g.c.g )
=> AD = ME
b) Gọi O là giao điểm của ED và AM
Nối AM
Xét tam giác AEM và tam giác MDA có:
^EAM = ^AMD ( so le trong vì EA // DM )
AM chung
^EMA = ^DAM ( so le trong vì EM // AD )
=> Tam giác AEM = tam giác MDA ( g.c.g )
=> AE = DM ( hai cạnh tương ứng )
Xét tam giác AEO và tam giác MDO có:
^AED = ^EDM ( so le trong vì AE // DM )
AE = DM ( chúng minh trên )
^EAM = ^AMD ( so le trong vì AE // DM )
=> Tam giác AEO = tam giác MDO ( g.c.g )
=> EO = OD
=> O là trung điểm ED. (1)
Mà OA = OM ( do tam giác AOE = tam giác DOM )
=> O là trung điểm của AM. (2)
Từ (1), (2) => O là trung điểm của ED và AM và là giao điểm của OE và AM
Mà I là trung điểm ED ( giả thiết )
=> Điểm O và I trùng nhau.
=> I là trung điểm của ED và AM, là giao điểm của AM và ED
=> 3 điểm A, I, M thẳng hàng

a: Xét tứ giác ABCD có
AD//BC
AB//CD
Do đó: ABCD là hình bình hành
Suy ra: BC=AD


a) Xét ΔCBM và ΔADM có:
AM=MC (giả thtết)
gócCMB=gócAMD ( đối đỉnh)
BM=MD (giả thiết)
⇒ ΔCBM=ΔADM (c.g.c)
BC=DA (hai cạnh tương ứng)
b) Xét ΔABM và ΔCDM có:
AM=CM (giả thiết)
gócAMB=gócCMD(đối đỉnh)
BM=DM (giả thiết)
⇒ ΔABM=ΔCDM (c.g.c)
gócBAM=gócDCM=90độ (hai góc tương ứng) (đpcm)
⇒ DC⊥AC (đpcm)
c) Ta có BN//AC mà AC⊥DC
⇒ BN⊥DC ⇒gócBND=90độ
AB//CD (do cùng ⊥AC)
Xét ΔABC và ΔNBC có:
gócABC=gócNCB (hai góc ở vị trí so le trong)
BC chung
gócACB=gócNBC (do BN//AC nên đó là hai góc ở vị trí so le trong)
⇒ ΔABC=ΔNBC (g.c.g)
⇒ AB=NC (hai cạnh tương ứng)
Xét ΔABM và ΔCNM có:
AB=CN (cmt)
góc BAM=gócNCM=90độ
góc BAM= gócNCM=90độ
AM=CM (giả thiết)
⇒ ΔABM=ΔCNM (đpcm)