Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABH vuông tại H và ΔDBH vuông tại H có
BH chung
HA=HD
Do đó: ΔABH=ΔDBH
b: Xét ΔABC và ΔDBC có
BA=BD
góc ABC=góc DBC
BC chung
Do đó: ΔABC=ΔDBC
=>góc BDC=90 độ
c: ΔABC=ΔDBC
nên góc ACB=góc DCB
=>CB là phân giác của góc ACD

a) Xét tam giác ABC cân tại A: AH là đường cao (AH vuông góc với BC)
=> AH là đường trung tuyến (TC tam giác cân)
=> H à TĐ của BC
=> BH = HC
Xét tam giác AHB và tam giác AHC:
BH = HC (cmt)
^AHB = ^AHC (90o)
AH chung
=> tam giác AHB = tam giác AHC (ch - cgv)
b) Ta có: HA = HD (gt) => H là TĐ của AD
Xét tam giác ACD có:
CH là đường cao (CH vuông góc AD)
CH là trung tuyến (H là TĐ của AD)
=> tam giác ACD cân tại C
c) Xét tam giác ACD cân tại A có:
AD > AC + CD (Bất đẳng thức trong tam giác)
=> \(\dfrac{1}{2}AD=\dfrac{1}{2}\left(AC+CD\right)\)
Mà \(HA=\dfrac{1}{2}AD\) (H là TĐ của AD)
=> \(HA>\dfrac{1}{2}\left(AC+CD\right)\) (ĐPCM)
Bạn có thể giúp mik thêm 1 cái nx là vẽ hình đc ko bạn?

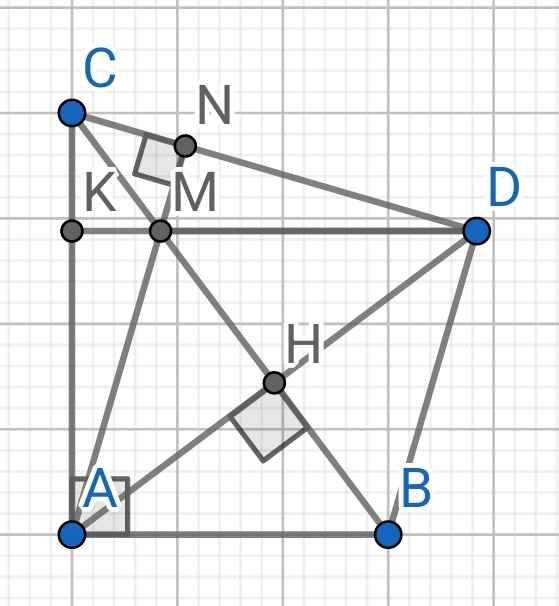 a) Sửa đề: Chứng minh ABH = DBH
a) Sửa đề: Chứng minh ABH = DBH
Giải:
Xét hai tam giác vuông: ∆ABH và ∆DBH có:
BH là cạnh chung
AH = DH (gt)
⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)
⇒ ∠ABH = ∠DBH (hai góc tương ứng)
⇒ BH là tia phân giác của ∠ABD
b) Do DM // AB (gt)
⇒ ∠MDH = ∠HAB (so le trong) (1)
Do ∆ABH = ∆DBH (cmt)
⇒ ∠HAB = ∠HDB (hai góc tương ứng) (2)
Từ (1) và (2) ⇒ ∠MDH = ∠HDB
Xét hai tam giác vuông: ∆DHM và ∆DHB có:
DH là cạnh chung
∠MDH = ∠HDB (cmt)
⇒ ∆DHM = ∆DHB (cạnh góc vuông - góc nhọn kề)
⇒ ∠DHM = ∠DHB (hai góc tương ứng)
Mà ∠DHM + ∠DHB = 180⁰ (kề bù)
⇒ ∠DHM = ∠DHB = 180⁰ : 2 = 90⁰
⇒ DH ⊥ BM (3)
Do ∆DHM = ∆DHB (cmt)
⇒ HM = HB
⇒ H là trung điểm của BM (4)
Từ (3) và (4) ⇒ HD là đường trung trực của BM
⇒ AD là đường trung trực của BM
c) Do AD là đường trung trực của BM (cmt)
⇒ AD ⊥ CH
Do DK // AB (gt)
⇒ DK ⊥ AC (AB ⊥ AC)
∆ACD có:
CH là đường cao (CH ⊥ AD)
DK là đường cao thứ hai (DK ⊥ AC)
⇒ AM là đường cao thứ ba
Mà AM ⊥ CN tại N
⇒ AN là đường cao thứ ba của ∆ACD
⇒ C, N, D thẳng hàng

mk chỉ vẽ hình thôi nha bạn nhiinf vào hình rồi giải
hình ko đc chuẩn lắm
Giải
a) Xét tam giác ABH và tam giác DBH có:
AH=DH(gt)
góc AHB=góc BHD (=90 độ)
BH cạnh chung
Vậy tam giác ABH=tam giác DBH (c.g.c)
b)Xét tam giác AHC và tam giác DHC có:
AH=DH(gt)
góc AHC= góc DHC (=90độ)
HC cạnh chung
Suy ra:tam giác AHC=tam giác DHC(c.g.c)
suy ra:AC=CD(2 cạnh t/ứ)