Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 Võ Hồng Nhung
Võ Hồng Nhung
1 phút trước (15:05)
Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của BC, AC, AB. Gọi O là 1 điểm bất kì. A' là điểm đối xứng với O qua D, B' là điểm đối xứng với O qua E, C' là điểm đối xứng với O qua F. Chứng minh AA', BB', CC' đồng quy tại 1 điểm.

A B C M N P Q I K D
Trên tia đối của MP lấy điểm D sao cho MP=MD.
Ta có: \(\Delta\)MBP=\(\Delta\)MCD (c.g.c) => BP=CD (2 cạnh tương ứng)
Mà BP=CQ => CD=CQ => \(\Delta\)DCQ cân tại C => ^CQD= (1800-^DCQ)/2
=> ^MPB=^MDC (2 góc tương ứng) ở vị trí so le trong => AB//CD => ^DCQ=^IAK (Đồng vị)
M là trung điểm PD, N là trung điểm PQ => MN là đường trung bình của \(\Delta\)PDQ
=> MN//DQ hay IK//DQ => ^CQD=^AKI (Đồng vị)
=> \(\Delta\)AIK có: ^AKI= (1800-^IAK)/2 = (1800-^DCQ)/2 = ^CQD
=> Tam giác AIK cân tại A (đpcm)
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

này cái bạn nguyễn xuân toàn kia bị gì thế ? họ là hỏi bài mà !

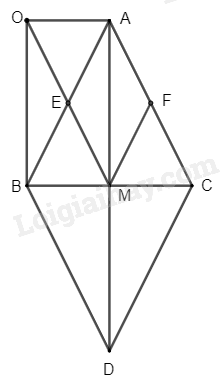
a) Xét tứ giác \(ABDC\) có:
\(M\) là trung điểm của \(BC\) (gt)
\(M\) là trung điểm của \(AD\) (do \(D\) đối xứng với \(A\) qua \(BC\))
Suy ra \(ABDC\) là hình bình hành
b) Do \(\Delta ABC\) cân tại \(A\), có \(AM\) là trung tuyến (gt)
Suy ra \(AM\) là đường cao, trung trực, phân giác
Suy ra \(AM\) vuông góc \(BM\) và \(CM\)
Xét tứ giác \(OAMB\) ta có:
\(E\) là trung điểm của \(OM\) và \(AB\) (gt)
Suy ra \(OAMB\) là hình bình hành
Suy ra \(OB\) // \(AM\); \(OA\) // \(MB\); \(OA = BM\); \(OB = AM\)
Mà \(AM \bot BM\) (cmt)
Suy ra: \(AM \bot OA\); \(OB \bot MB\)
Mà \(AM\) // \(OB\) (cmt)
Suy ra \(OB \bot OA\)
Xét \(\Delta AOB\) và \(\Delta MBO\) (các tam giác vuông) ta có:
\(\widehat {{\rm{AOB}}} = \widehat {{\rm{OBM}}} = 90^\circ \)
\(AO = MB\) (cmt)
\(OB = AM\) (cmt)
Suy ra \(\Delta AOB = \Delta MBO\) (c-g-c)
Suy ra \(OM = AB\)
c) \(OM = AB\) (cmt)
Mà \(EM = EO = \frac{1}{2}OM\); \(EA = EB = \frac{1}{2}AB\)
Suy ra \(EO = EA = EM = EB\) (1)
Xét \(\Delta ABC\) cân ta có: \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)
Mà \(EA = EB = \frac{1}{2}AB\); \(FA = FC = \frac{1}{2}AC\) (gt)
Suy ra \(AE = EB = FA = FM\) (2)
Xét \(\Delta BEM\) và \(\Delta CMF\) ta có:
\(BE = CF\) (cmt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)
\(BM = CM\) (gt)
Suy ra \(\Delta BEM = \Delta CFM\) (c-g-c)
Suy ra \(EM = FM\) (3)
Từ (1), (2), (3) suy ra \(AE = AF = FM = ME\)
Suy ra \(AEMF\) là hình thoi
Để chứng minh \(A A^{'}\), \(B B^{'}\), và \(C C^{'}\) đồng quy, ta sẽ sử dụng tính chất của các điểm trung điểm và các đoạn thẳng đồng quy trong hình học phẳng, cụ thể là các trung tuyến của tam giác.
Giả thiết:
Ta cần chứng minh rằng các đường thẳng \(A A^{'}\), \(B B^{'}\), và \(C C^{'}\) đồng quy.
Bước 1: Tính chất của các trung điểm
Theo giả thiết, ta có:
Bước 2: Xây dựng các vectơ liên quan đến \(A A^{'}\), \(B B^{'}\), \(C C^{'}\)
\(\overset{\rightarrow}{A^{'}} = 2 \overset{\rightarrow}{D} - \overset{\rightarrow}{O}\)
\(\overset{\rightarrow}{B^{'}} = 2 \overset{\rightarrow}{E} - \overset{\rightarrow}{O}\)
và
\(\overset{\rightarrow}{C^{'}} = 2 \overset{\rightarrow}{F} - \overset{\rightarrow}{O}\)
Bước 3: Mối quan hệ giữa các điểm
Ta có thể xét các vectơ chỉ phương của các đường thẳng \(A A^{'}\), \(B B^{'}\), và \(C C^{'}\). Để các đường thẳng này đồng quy, chúng ta cần chứng minh rằng chúng đều đi qua một điểm duy nhất, hay nói cách khác, chúng phải có một điểm chung.
Trong trường hợp này, các đường thẳng \(A A^{'}\), \(B B^{'}\), và \(C C^{'}\) là các đường đồng quy của tam giác, và do tính chất của các trung điểm và các điểm trung gian, ta có thể áp dụng định lý Ceva trong trường hợp tam giác. Định lý Ceva nói rằng nếu một số đường thẳng trong tam giác đồng quy, thì tích các tỷ lệ phân chia các cạnh của tam giác theo các đường thẳng đó bằng 1.
Bước 4: Áp dụng định lý Ceva
Vì các đường thẳng \(A A^{'}\), \(B B^{'}\), và \(C C^{'}\) là các đoạn nối từ các đỉnh của tam giác đến các điểm trên các cạnh của tam giác, và các điểm \(D\), \(E\), \(F\) là các trung điểm của các cạnh của tam giác, ta có thể áp dụng định lý Ceva trong trường hợp các đường thẳng này đồng quy.
Kết luận:
Vì các điều kiện đã được thỏa mãn và ta có thể áp dụng định lý Ceva, ta kết luận rằng ba đường thẳng \(A A^{'}\), \(B B^{'}\), và \(C C^{'}\) đồng quy tại một điểm.