Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C O
Ta có: AB < OA + OB (bất đẳng thức tam giác)
AC < OA + OC (bất đẳng thức tam giác)
BC < OB + OC (bất đẳng thức tam giác)
=> AB + AC + BC < 2 (OA + OB + OC) => \(\frac{AB+AC+BC}{2}< OA+OB+OC\)(1)
và OA + OB < BC + AC (kết quả của bài 17 SGK)
OB + OC < AB + AC (kết quả của bài 17 SGK)
OA + OC < AB + BC (kết quả của bài 17 SGK)
=> 2 (OA + OB + OC) < 2 (AB + AC + BC) => OA + OB + OC < AB + AC + BC (2)
Từ (1) và (2) => \(\frac{AB+AC+BC}{2}< OA+OB+OC< AB+AC+BC\)(đpcm)

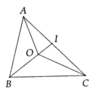
A B C O I
Theo bất đẳng thức tam giác ta có
\(\Delta OAB:\)\(AB< OA+OB\)
\(\Delta OAC:\)\(AC< OA+OC\)
\(\Delta OBC:\)\(BC< OB+OC\)
\(\Rightarrow AB+BC+AC< 2\left(OA+OB+OC\right)\)
\(\Leftrightarrow\frac{AB+BC+AC}{2}< OA+OB+OC\)(1)
Gọi I là giao điểm của BO và AC
\(\Delta OAI:-OA< AI+OI\)
\(\Delta IBC:-IB< IC+BC\)
\(\Rightarrow OA+IB< AI+OI+IC+BC=AC+BC+OI\)
\(\Leftrightarrow OA+IB-OI< AC+BC\)
\(\Leftrightarrow OA+OB< AC+BC\)(OI+OB=IB)
Chứng minh tương tự ta có \(OA+OC< AB+BC;OB+OC< AB+AC\)
\(\Rightarrow2\left(OA+OB+OC\right)< 2\left(AB+BC+AC\right)\)(CỘNG 2 VẾ CỦA 3 BẤT ĐẢNG THỨC TRÊN)
\(\Leftrightarrow OA+OB+OC< AB+BC+AC\)(2)
Từ (1),(2) suy ra điều phải chứng minh.

 tham khảo nha
tham khảo nha