Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ thấy tam giác MBI đồng dạng với tam giác MAB ( góc MBI = góc MAB; góc BMI chung)
suy ra MB/MA=MI/MB suy ra MB2= MA.MI
suy ra MC2= MA.MI ( vì MB=MC) do đó MC/MA=MI/MC
Dẫn đến tam giác MCI đồng dạng với tam giác MAC suy ra đpcm

a) dựa vào tính chất đường phân giác" BM/BD=AM/AD" và "MC/EC=AM/AE"
bạn rút 2 vế ra được..."BM/AM=BD/AD=EC/AE" ( mà MC=BM)
dựa theo tính chất talet đảo => DE//BC
tk nha bạn
thank you bạn
(^_^)

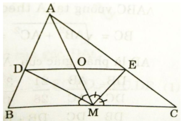
a) Vì AM là trung tuyến của \(\Delta ABC\Rightarrow BM=CM;M\in BC\)
Xét \(\Delta ABM\)có MD là p/g \(\widehat{BMA}\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\)hay \(\frac{AD}{BD}=\frac{AM}{CM}\left(1\right)\)
Xét \(\Delta ACM\)có ME là p/g \(\widehat{CMA}\Rightarrow\frac{AE}{CE}=\frac{AM}{CM}\left(2\right)\)
Từ (1)(2)\(\Rightarrow\frac{AD}{BD}=\frac{AE}{CE}\Rightarrow DE//BC\)(đ/ lí Ta-lét đảo)
b) Có \(DE//BC\), \(O\in DE,M\in BC\Rightarrow OD//BM;OE//CM\)
Xét \(\Delta ABM\)có \(OD//BM\Rightarrow\frac{OD}{BM}=\frac{OA}{AM}\left(3\right)\)
Xét \(\Delta ACM\)có \(OE//CM\Rightarrow\frac{OE}{CM}=\frac{OA}{AM}\left(4\right)\)
Từ (3)(4) \(\Rightarrow\frac{OD}{BM}=\frac{OE}{CM}\).Mà BM=CM \(\Rightarrow OD=OE\)

a) DM là đường phân giác của ΔABM nên theo tính chất đường phân giác của tam giác ta có:
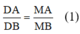
Tương tự EM là đường phân giác ΔACM nên:
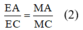
Mà MB = MC nên từ (1) và (2) suy ra

![]()
![]()
![]()
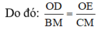
![]()

a, Vì MD là phân giác AMB \(\Rightarrow\frac{AD}{AM}=\frac{BD}{BM}\)\(\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\)\(\Rightarrow\frac{AD}{BD}=\frac{AM}{CM}\)(MB = MC)
Vì ME là phân giác AMC \(\Rightarrow\frac{AE}{AM}=\frac{EC}{MC}\)\(\Rightarrow\frac{AE}{EC}=\frac{AM}{MC}\)
\(\Rightarrow\frac{AE}{EC}=\frac{AD}{BD}\) => DE // BC (định lý Thales đảo)
b, Vì DE // BE (cmt) \(\Rightarrow\frac{DO}{BM}=\frac{AO}{OM}\)(Hệ quả định lý Thales) và \(\frac{OE}{MC}=\frac{OA}{OM}\) (Hệ quả định lý Thales)
\(\Rightarrow\frac{DO}{BM}=\frac{OE}{MC}\)
Mà BM = MC (gt)
=> DO = OE

a: Xét ΔMAB có MD là phan giác
nên MA/MB=AD/DB=MA/MC
Xét ΔMAC có ME là phân giác
nên MA/MC=AE/EC
=>AD/DB=AE/EC
=>DE//BC
b: Xét ΔAMB có OD//MB
nên OD/MB=AO/AM
Xét ΔAMC có OE//MC
nên OE/MC=AO/AM
=>OD/MB=OE/MC
mà MB=MC
nên OD=OE

1) \(A=\frac{x^2+2x+9}{-2y-y^2+3}=\frac{\left(x^2+2x+1\right)+\left(2y^2+4y+2\right)+2\left(-y^2-2y+3\right)}{-y^2-2y+3}=\frac{\left(x+1\right)^2+2\left(y+1\right)^2}{-y^2-2y+3}+2\ge2\)Vậy Min A = 2 \(\Leftrightarrow\hept{\begin{cases}x=-1\\y=-1\end{cases}}\)

1a) A=D=E=90 độ
=>AEHD là hcn
=>AH=DE
b)Xét tam giác DBH vuông tại D có:
DI là đường trung tuyến ứng với cạnh huyền BH
=>DI=BH/2=IH
=>tam giác IDH cân tại I
=>góc IDH=góc IHD (1)
Gọi O là gđ 2 đường chéo AH và DE
=>OD=OA=OE=OH (tự c/m)
=> tam giác DOH cân tại O
=> góc ODH=góc OHD(2)
từ (1) và (2) => góc ODH+góc IDH=90 độ(EHD+DHI=90 độ)
=>IDvuông góc DE(3)
Cmtt ta được: KEvuông góc DE(4)
Từ (3)và (4) => DI//KE.
2a) Ta có góc HAB+góc HAC=90 độ (1)
Xét tam giác ABC vuông tại A có
AM là đg trung tuyến ứng vs cạnh huyền BC
=>AM=MC
=>tam giác AMC cân
=>góc MAC=góc ACM
Lại có: góc HAC+góc ACH=90 độ(2)
Từ (1) và (2) => góc BAH=góc ACM
Mà góc AMC=góc MAC(cmt)
=>ABH=MAC(3)
b)A=D=E=90 độ
=>AFHE là hcn
Gọi O là gđ EF và AM
OA=OF(tự cm đi nha)
=>tam giác OAF cân
=>OAF=OFA(4)
Ta có : OAF+MCA=90 độ(5)
Từ (3)(4) và (5)
=>MAC+OFA=90 độ
Hay AM vuông góc EF
k giùm mình nha.