

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
=>ΔABC=ΔADE
=>BC=DE
b: Gọi giao của BD với CE là M
góc MEB+góc MBE
=45+45=90 độ
=>BD vuông góc CE tại M
Xét ΔCEB có
CA,BM là đường cao
CA cắt BM tại D
=>D là trực tâm
=>BC vuông góc ED

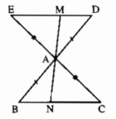
ΔABC và ΔADE có:
AB = AD (gt)
AC = AE (gt)
∠BAC = ∠DAE (hai góc đối đỉnh)
⇒ ΔABC = ΔADE (c.g.c)
⇒ ∠C = ∠E ⇒ DE // BC.

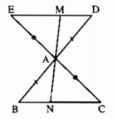
ΔAEM và ΔACN có:
∠C = ∠E ( hai góc so le trong, DE// BC)
AE = AC ( giả thiết)
∠EAM = ∠CAN (hai góc đối đỉnh)
⇒ ΔAEM = ΔACN (g.c.g) ⇒ AM = AN ( hai cạnh tương ứng).

tg ADE=ABC( AB=AD;AC=AE;A đối đỉnh)
=>gocE=C
xet tg AEN va tgACM bằng nhau( CM=EN;AE=AC;E=C)
=> goc NAE=CAM ( 2 goc nay o vi tri đối đỉnh nên M;A;N

cho tam giác abc, AB=4,8cm; BC=3,6cm; AC= 6,4cm. trên AC lấy điểm E sao cho AE=2,4cm; trên AB lấy điểm D sao cho AD= 3,2 cm. gọi giao điểm của BC với ED là F. tính DF