Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: Xét ΔOHA vuông tại A và ΔOHB vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOHA=ΔOHB
Suy ra: HA=HB
hay ΔHAB cân tại H
b: Xét ΔOAB có
OH là đường cao
AD là đường cao
OH cắt AD tại C
Do đó: C là trực tâm của ΔOAB
Suy ra: BC\(\perp\)Ox
c: \(\widehat{HOA}=\dfrac{60^0}{2}=30^0\)
Xét ΔOHA vuông tại A có
\(\cos HOA=\dfrac{OA}{OH}\)
\(\Leftrightarrow OA=\dfrac{\sqrt{3}}{2}\cdot4=2\sqrt{3}\left(cm\right)\)

Mình vẫn chưa thấy vai trò của $M,N$ trong bài toán này. Bạn xem lại đề.

Lời giải:
Vì $M,N$ lần lượt là trung điểm của $AB,AC$ nên $MN$ là đường trung bình ứng với cạnh $BC$ của tam giác $ABC$
$\Rightarrow MN\parallel BC$ và $MN=\frac{1}{2}BC$
$\Rightarrow \overrightarrow{MN}=\frac{1}{2}\overrightarrow{BC}$
Mà:
$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}$ do $P$ là trung điểm $BC$
Do đó: $\overrightarrow{MN}=\overrightarrow{BP}$
---------------------------
Dễ chứng minh $NP$ là đường trung bình ứng với cạnh $AB$
$\Rightarrow \overrightarrow{PN}=\frac{1}{2}\overrightarrow{BA}$
Mà $M$ là trung điểm $AB$ nên $\overrightarrow{MA}=\frac{1}{2}\overrightarrow{BA}$
Vậy: $\overrightarrow{MA}=\overrightarrow{PN}$

Đáp án A
Ta có 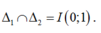
Vì A thuộc ∆1 nên A( a; a+ 1).
Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).
Mặt khác:
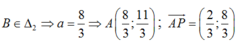
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:
4x – y- 7 = 0