Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta EBCcó:BE=BC\left(gt\right)\)
\(\Rightarrow\Delta EBC\) cân tại B
\(\Rightarrow\) góc E = góc C
Ta có : góc ABD + góc DBC + góc CBE = 1800 (kề bù)
\(\Rightarrow\) góc CBE = 1800 - ( góc ABD + góc DBC)
Và ta lại có: góc E + góc CBE + góc C = 1800 (tổng 3 góc trong tam giác EBC)
\(\Rightarrow\) góc CBE = 1800 - ( góc E + góc C)
Mà : góc ABD = góc DBC ( vì BD là tia phân giác của góc ABC)
góc E = C ( cmt )
\(\Rightarrow\) góc DBC = góc C
Mà : 2 góc này nằm ở vị trí so le trong
\(\Rightarrow BDsong^2EC\)

a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
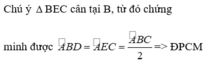
Xét tam giác BCE có BC=BE => tam giác BCE cân tại B.
do đó góc C=E. ( T/C tam giác cân )
ta có : B1+B2+B3=180o
C+E+B =180o
Mà góc C=E ; B1=B2 (VÌ BD là phân giác của góc B)
=> GÓC 2C=180=2B2
=> 2C=2B2
=> C=B2
Mà chúng ở vị chí so le trong
=> BD // CE (đpcm)
A B C D E 1 2 3
thank kiu nhóa lêminhduc