Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: Xét tứ giác BPCE có
Q là trung điểm của BC
Q là trung điểm của PE
Do đó: BPCE là hình bình hành
Suy ra: BP=CE
hay CE=AP
b: Ta có: AP//EC
nên \(\widehat{APC}=\widehat{ECP}\)
c: Xét ΔABC có
P là trung điểm của AB
Q là trung điểm của BC
Do đó: PQ là đường trung bình
=>PQ//AC và PQ=AC/2
a: Xét tứ giác ABCP có
F là trung điểm chung của AC và BP
=>ABCP là hình bình hành
=>AP=BC và AP//BC
b: Xét tứ giác AQBC có
E là trung điểm chung của AB và QC
=>AQBC là hình bình hành
=>AQ//BC và AQ=BC
=>AP=AQ và AP//AQ
=>A là trung điểm của PQ
c: BA+BC=BC+CP>CP=2BF
Mình không vẽ hình, bạn tự vẽ nhé!
a) M là trung điểm của BC \(\Rightarrow BM=MC\)
Xét \(\Delta BAM\)và \(\Delta CDM\)có:
MA=MD ( giả thiết )
\(\widehat{BMA}=\widehat{CMD}\)( tính chất đối đỉnh )
BM=MC ( chứng minh trên )
\(\Rightarrow\Delta BAM=\Delta CDM\)( c.g.c )
b) Xét \(\Delta ACM\)và \(\Delta DBM\)có:
MA=MD ( giả thiết )
\(\widehat{BMD}=\widehat{CMA}\)( tính chất đối đỉnh )
BM=MC ( chứng minh trên )
\(\Rightarrow\Delta ACM=\Delta DBM\)( c.g.c )
\(\Rightarrow AC=BD\)( 2 cạnh tương ứng )
\(\Rightarrow\widehat{MAC}=\widehat{MDB}\)( 2 góc tương ứng ) ở vị trí so lê trong
\(\Rightarrow\)AC//BD
c) Đề bài không rõ ràng mình không làm được
d) Đề bài không rõ ràng mình không làm được
Chúc bạn học tốt!
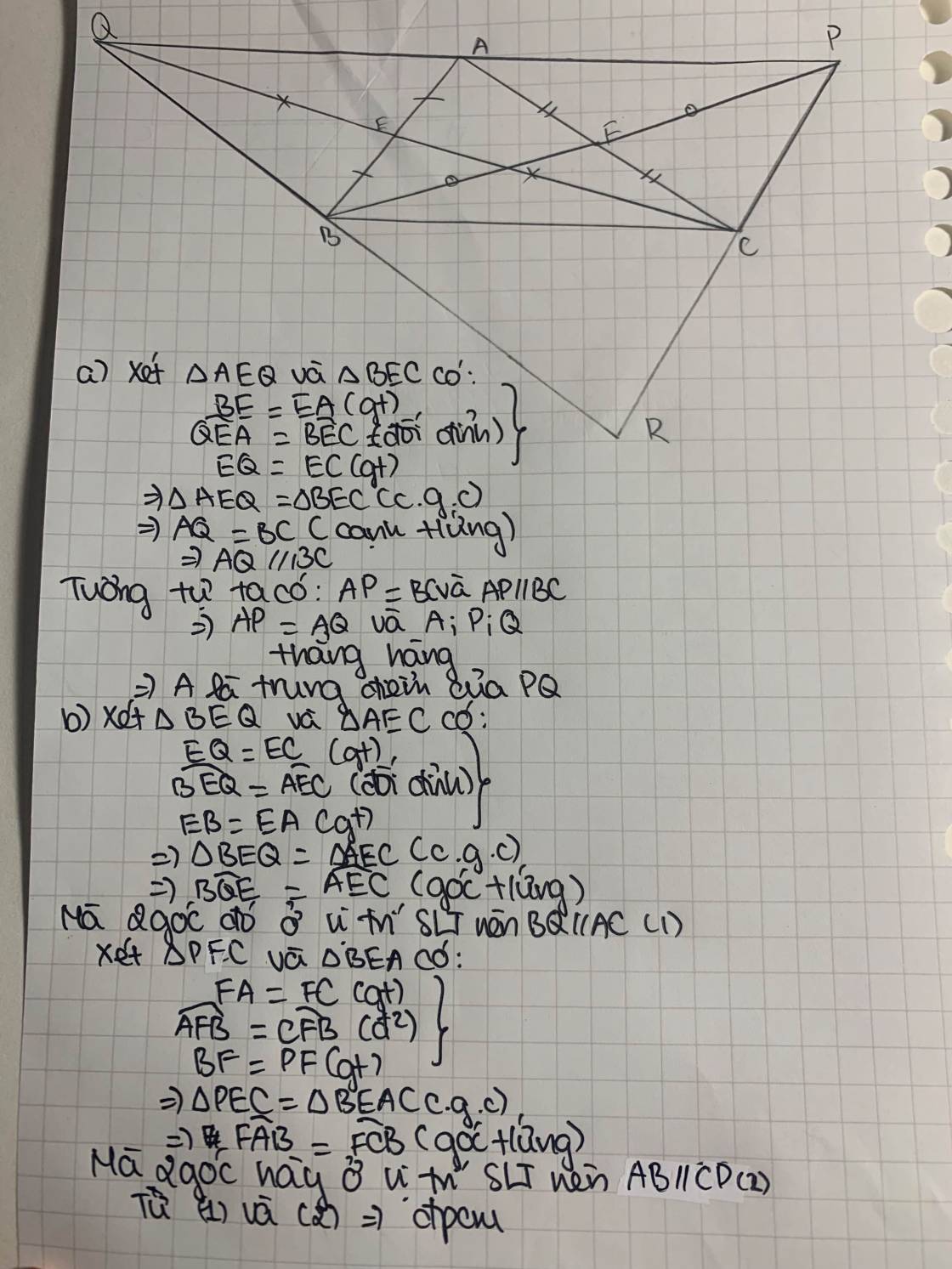
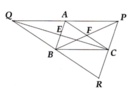
a) Xét tam giác AEQ và tam giác BEC có
EQ=EC
AEQ=BEC đối đỉnh
EA=EB
=> tam giác AEQ = tam giác BEC(c.g.g).
=> AQ=BC(cạnh tuognư ứng). (1)
Xét Tam giác AFP và tam giác CFB có
AF=CF
AFP=CFB đối đỉnh
FB=FP
=> tam giác AFB = tam giác CFB(c.g.c)
=> AP = BC (2)
từ (1) và (2) suy ra AP=AQ.
