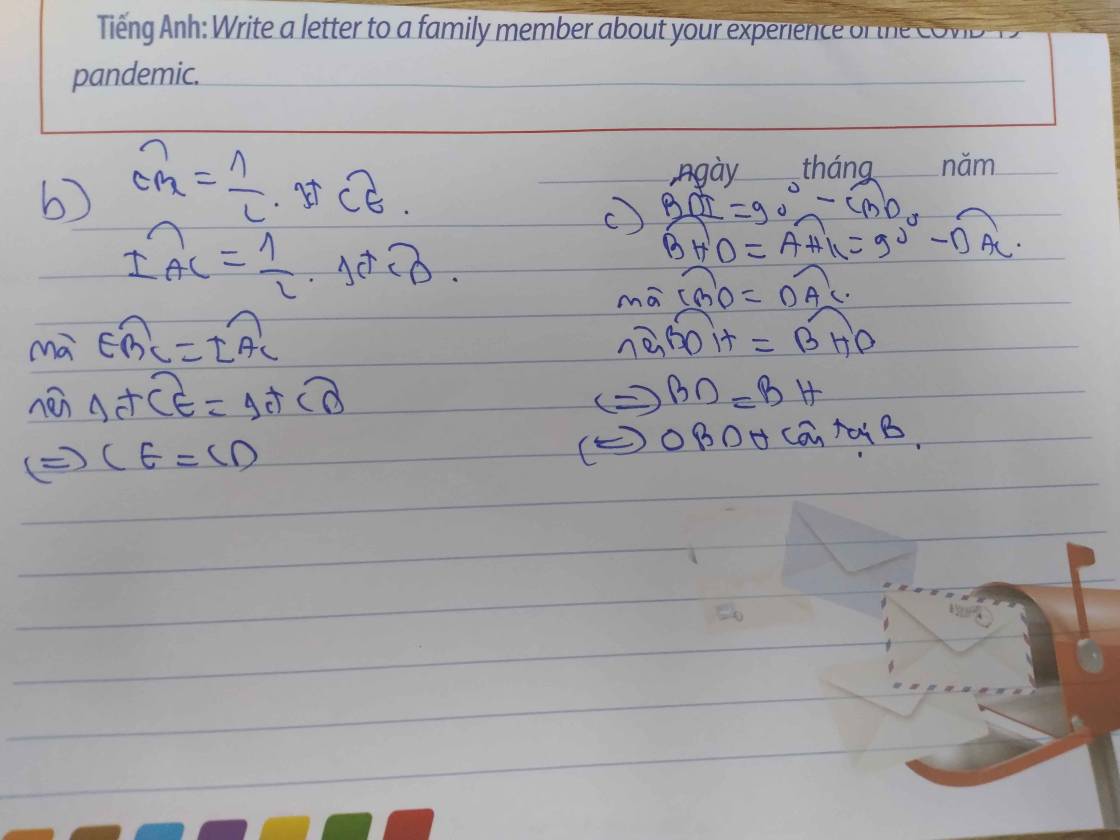Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

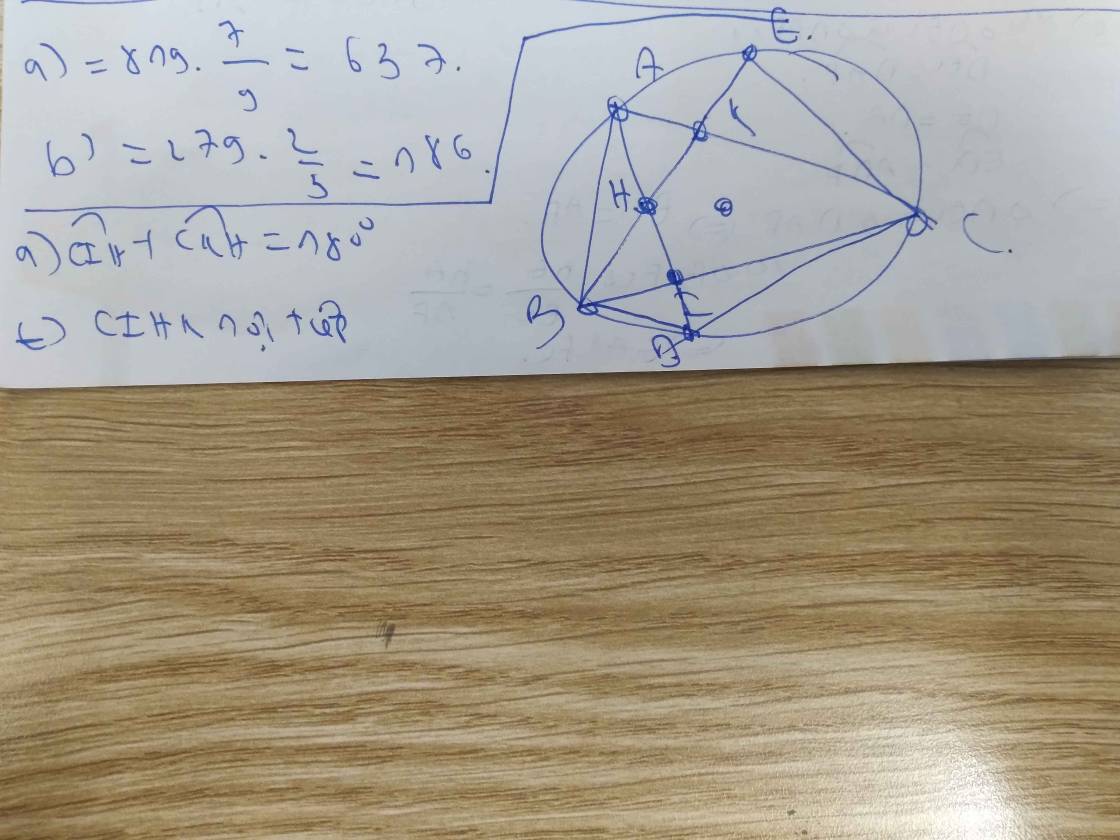
a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CED=góc CAD
góc CDE=góc CAE
mà góc CAD=góc CAE(=góc CBD)
nên góc CED=góc CDE
=>CD=CE

a: góc HMC+góc HNC=180 độ
=>HMCN nội tiếp
b: góc CAD=góc NBC
=>1/2*sđ cung CD=1/2*sđ cung CE
=>CD=CE
c: góc BHM=góc BCN=1/2*sđ cung BA
góc BDH=1/2*sđ cung BA
=>góc BHD=góc BDH
=>ΔBHD cân tại B

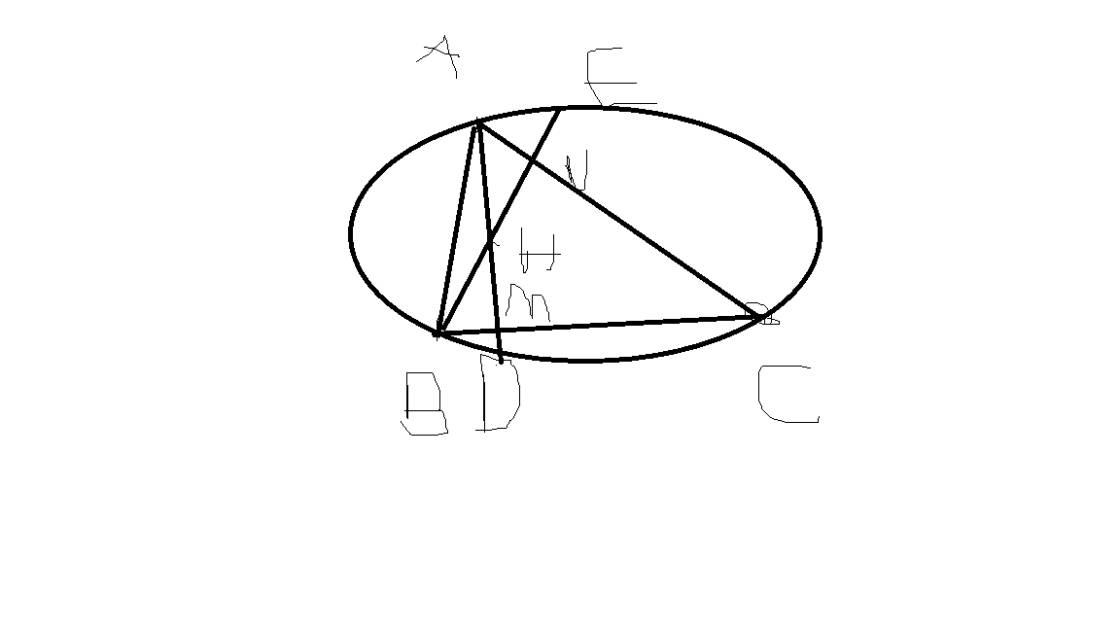
a) * Cách 1.

b) Do 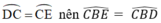 ( hai góc nội tiếp chắn hai cung bằng nhau).
( hai góc nội tiếp chắn hai cung bằng nhau).
Suy ra: BC là tia phân giác của góc 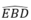 .
.
Xét tam giác BHD có BA’ vừa là đường cao vừa là đường phân giác nên tam giác BHD cân tại B.


a: Xét tứ giác HMCN co
góc HMC+góc HNC=180 đô
=>HMCN là tứ giác nội tiếp
b: góc CBE=1/2*sđ cung CE
góc CAD=1/2*sđ cung CD
mà góc CBE=góc CAD
nên CE=CD
c: góc BHD=góc ACB=1/2*sđ cung AB=góc BDH
=>ΔBHD cân tại B

Lời giải:
* Bạn tự vẽ hình nha *
a) Xét tứ giác $A'HB'C$ có tổng hai góc đối nhau:
\(\widehat{HA'C}+\widehat{HB'C}=90^0+90^0=180^0\) nên \(A'HB'C\) là tứ giác nội tiếp.
Xét tứ giác $AB'A'B$ có: \(\widehat{AB'B}=\widehat{AA'B}=90^0\) cùng nhìn cạnh $AB$ nên $AB'A'B$ là tứ giác nội tiếp
b)
Theo phần a ta đã chứng minh được \(AB'A'B\) nội tiếp, do đó \(\widehat{B'AA'}=\widehat{B'BA'}\) (hai góc nội tiếp cùng nhìn cung $A'B'$ )
Mà: \(\widehat{B'AA'}=\widehat{CAD}=\frac{1}{2}\text{cung CD}\)
\(\widehat{B'BA'}=\widehat{EBC}=\frac{1}{2}\text{cung CE}\)
Do đó: \(\frac{1}{2}\text{cung CD}=\frac{1}{2}\text{ cung CE}\Rightarrow CD=CE\)

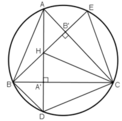
* Cách 1.
Ta có: AD vuông BC tại A' nên A A ' B ^ = 90 o
Vì A A ' B ^ là góc có đỉnh bên trong đường tròn nên:
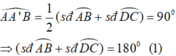
Tương tự, vì BE vuông góc AC tại B' nên ta có:
E B ' C ^ là góc có đỉnh nằm trong đường tròn
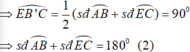
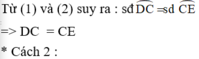
Ta có:![]() (1)
(1)
Và ![]() (2)
(2)
Tà (1) và (2) ![]()
Đây là hai góc nội tiếp chắc hai cung DC và CE nên:
![]()