Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C I H K D E M N
Bổ đề 1: Xét tứ giác MNPQ là tứ giác lồi có MP giao NQ tại R. Gọi H,K lần lượt là trực tâm của tam giác MRN;PRQ. U và V lần lượt là trung điểm của NP và MQ. Khi đó UV vuông góc với HK.
Bổ đề 2: Xét tam giác ABC nội tiếp (O), L là điểm chính giữa cung BAC. Lấy X thuộc cạnh AB, Y thuộc cạnh AC sao cho BX = CY. Khi đó LX = LY.
Hai bổ đề trên rất quen thuộc, các bạn tự chứng minh.
Giải bài toán: Đặt M,N thứ tự là trung điểm của BD,CE. Ta có BM = CN (= BD/2 = CE/2)
Gọi K là trung điểm cung BAC. Theo Bổ đề 2 thì KM = KN (1)
Dễ thấy ID = IC; IB = IE; BD = CE. Suy ra \(\Delta\)BID = \(\Delta\)EIC (c.c.c)
Hai tam giác trên có trung tuyến tương ứng là IM,IN. Do đó IM = IN (2)
Để ý rằng I là trực tâm của \(\Delta\)BFC. Áp dụng Bổ đề 1 vào tứ giác BDEC ta được IH vuông góc MN (3)
Từ (1);(2) và (3) suy ra ba điểm I,H,K thẳng hàng. Đó là điều phải chứng minh.

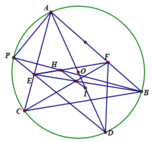
A B C O G I K L D E F M N P e
Gọi tiếp điểm của (I) với BC,CA,AB thứ tự là D,E,F. G là trọng tâm của \(\Delta\)DEF.
Kéo dài AI,BI,CI cắt (O) lần lượt tại M,N,P (A khác M, B khác N, C khác P)
Dễ dàng chứng minh M,N,P lần lượt là điểm chính giữa các cung BC,CA,AB của (O)
Từ đó OM,ON,OP lần lượt vuông góc với BC,CA,AB và I là trực tâm của \(\Delta\)MNP
Ta có \(\Delta\)MNP với tâm ngoại tiếp O và trực tâm I, suy ra \(\overrightarrow{OI}=\overrightarrow{OM}+\overrightarrow{ON}+\overrightarrow{OP}\)
Chú ý rằng \(\overrightarrow{OM}=OM.\frac{\overrightarrow{ID}}{ID}=\frac{R}{r}\overrightarrow{ID}\). Từ đây \(\overrightarrow{OI}=\frac{R}{r}\left(\overrightarrow{ID}+\overrightarrow{IE}+\overrightarrow{IF}\right)\)
Lại có G là trọng tâm của \(\Delta\)DEF nên \(\overrightarrow{3IG}=\overrightarrow{ID}+\overrightarrow{IE}+\overrightarrow{IF}\)
Do đó \(\overrightarrow{OI}=\frac{3R}{r}\overrightarrow{IG}\), suy ra ba điểm O,I,G thẳng hàng (1)
Mặt khác, khi ta dựng vector đơn vị \(\overrightarrow{e}\)vuông góc với KL là hướng ra ngoài tứ giác BKLC
Thì \(KL.\overrightarrow{e}+BK.\overrightarrow{IF}+CL.\overrightarrow{IE}+BC.\overrightarrow{ID}=\overrightarrow{0}\)(ĐL Con Nhím)
Suy ra \(KL.\overrightarrow{e}+3BC.\overrightarrow{IG}=\overrightarrow{0}\)hay \(\overrightarrow{GI}=\frac{KL}{3BC}.\overrightarrow{e}\). Do vậy \(\overrightarrow{GI}\)// \(\overrightarrow{e}\)
Mà \(\overrightarrow{e}\)vuông góc với KL nên GI vuông góc KL (2)
Từ (1) và (2) suy ra OI cũng vuông góc với KL (đpcm).

1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.
Ta có A P H ^ = A E H ^ (góc nội tiếp)
= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)
⇒ P H ≡ P B
2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^
Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF
Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF
Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Do I là tâm nội tiếp nên EI là tia phân giác trong.
Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B
Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.