Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

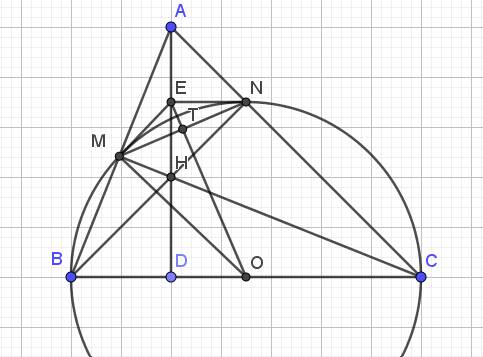
a: Xét tứ giác BMNC có
\(\widehat{BMC}=\widehat{BNC}=90^0\)
Do đó: BMNC là tứ giác nội tiếp

Lời giải:
a. Ta có:
$\widehat{BNC}=\widehat{BMC}=90^0$ (góc nt chắn nửa đường tròn - cung BC)
$\Rightarrow BN\perp AC, CM\perp AB$
Tam giác $ABC$ có 2 đường cao $BN, CM$ cắt nhau tại $H$ nên $H$ là trực tâm của tam giác $ABC$.
b. Gọi $D$ là giao của $AH$ và $BC$. Do $H$ là trực tâm tam giác $ABC$ nên $AH\perp BC$ tại $D$.
Tam giác $BMC$ vuông tại $M$
$\Rightarrow$ trung tuyến $MO= \frac{BC}{2}=BO$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow BOM$ là tam giác cân tại $O$
$\Rightarrow \widehat{OMB}=\widehat{OBM}=90^0-\widehat{BCM}$
$=90^0-\widehat{DCH}=\widehat{MHA}=\widehat{MHE}(1)$
$CM\perp AB$ nên $AMH$ là tam giác vuông tại $M$
$\Rightarrow ME=\frac{AH}{2}=EH$ (đường trung tuyến ứng với cạnh huyền bằng 1/2 cạnh huyền)
$\Rightarrow MEH$ cân tại $E$
$\Rightarrow \widehat{MHE}=\widehat{EMH}(2)$
Từ $(1); (2)\Rightarrow \widehat{OMB}=\widehat{EMH}$
$\Rightarrow \widehat{OMB}+\widehat{OMC}=\widehat{EMH}+\widehat{OMC}$
$\Rightarrow \widehat{BMC}=\widehat{EMO}$
$\Rightarrow \widehat{EMO}=90^0$
$\Rightarrow EM\perp MO$ nên $EM$ là tiếp tuyến $(O)$
c.
Ta có:
$EM=\frac{AH}{2}=EN$
$OM=ON$
$\Rightarrow EO$ là trung trực của $MN$
Gọi $T$ là giao điểm $EO, MN$ thì $EO\perp MN$ tại $T$ và $T$ là trung điểm $MN$.
Xét tam giác $EMO$ vuông tại $M$ có $MT\perp EO$ thì:
$ME.MO = MT.EO = \frac{MN}{2}.EO$
$\Rightarrow 2ME.MO = MN.EO$

a) Ta có: \(\widehat{AMO}=\widehat{ADO}=\widehat{ANO}=90^o\) nên \(M,N,D\) cùng nhìn \(AO\) dưới một góc vuông suy ra \(M,D,O,N,A\) cùng thuộc một đường tròn.
b) Gọi \(F\) là giao điểm của \(AC\) và đường tròn \(\left(O\right)\).
\(\Delta ANF\sim\Delta ACN\left(g.g\right)\) suy ra \(AN^2=AC.AF\).
Xét tam giác \(AHN\) và tam giác \(AND\):
\(\widehat{HAN}=\widehat{NAD}\) (góc chung)
\(\widehat{ANH}=\widehat{ADN}\) (vì \(AMDON\) nội tiếp, \(\widehat{ANH},\widehat{ADN}\) chắn hai cung \(\stackrel\frown{AM},\stackrel\frown{AN}\) mà \(AM=AN\))
\(\Rightarrow\Delta AHN\sim\Delta AND\left(g.g\right)\)
suy ra \(AN^2=AH.AD\)
suy ra \(AC.AF=AH.AD\)
\(\Rightarrow\Delta AFH\sim\Delta ADC\left(c.g.c\right)\Rightarrow\widehat{AFH}=\widehat{ADC}=90^o\)
suy ra \(\widehat{HFC}=90^o\) mà \(\widehat{BFC}=90^o\) (do \(F\) thuộc đường tròn \(\left(O\right)\))
suy ra \(B,H,F\) thẳng hàng do đó \(BH\) vuông góc với \(AC\).
Tam giác \(ABC\) có hai đường cao \(AD,BF\) cắt nhau tại \(H\) suy ra \(H\) là trực tâm tam giác \(ABC\).

a: Gọi I là trung điểm của CM
Xét (I) có
ΔCDM nội tiếp
CM là đường kính
Do đó: ΔCDM vuông tại D
=>góc CDM=góc CDB=90 độ
Xét tứ giác ABCD có
góc CAB=góc CDB=90 độ
=>ABCD nội tiếp
b: Xét ΔCAB có CO/CB=CM/CA=1/2
nên OM//AB
=>OM vuông góc AC tại M
=>OM là tiếp tuyến của (I)
a) Để chứng minh A, B, C, D cùng thuộc một đường tròn, ta cần chứng minh tứ giác ABCD là tứ giác nội tiếp. Ta có:
- Góc BAD = góc BAC (cùng chắn cung BC)
- Góc BCD = góc BCA (cùng chắn cung BA)
Do đó, góc BAD + góc BCD = góc BAC + góc BCA = 90 độ (vì tam giác ABC vuông tại A)
Suy ra, tứ giác ABCD là tứ giác nội tiếp.
b) Để chứng minh OM là tiếp tuyến của đường tròn đường kính MC, ta cần chứng minh OM vuông góc với MC. Ta có:
- Góc OMB = góc ONB (cùng chắn cung OB)
- Góc ONB = góc MNB (do tam giác MNB vuông tại N)
- Góc MNB = góc MCB (do tam giác MCB vuông tại C)
- Góc MCB = góc ACB (do tam giác ABC vuông tại A)
Do đó, góc OMB = góc ACB
Suy ra, OM vuông góc với MC.
Vậy OM là tiếp tuyến của đường tròn đường kính MC.

a, Vì \(\widehat{BMC}=\widehat{BNC}=90^0\) (góc nt chắn nửa đg tròn) nên BN,CM là đường cao tam giác ABC
Do đó H là trực tâm tam giác ABC
Vậy AH là đường cao thứ 3 hay AH⊥BC tại D
b, \(OC=ON\Rightarrow\widehat{ONC}=\widehat{OCN}\)
Mà NE là trung tuyến ứng cạnh huyền tg AHN nên \(NE=EH\)
\(\Rightarrow\widehat{ANE}=\widehat{EAN}\)
\(\Rightarrow\widehat{ANE}+\widehat{ONC}=\widehat{OCN}+\widehat{EAN}=90^0\left(\Delta ADC\perp D\right)\\ \Rightarrow\widehat{ENO}=180^0-\left(\widehat{ANE}+\widehat{ONC}\right)=90^0\\ \Rightarrow EN\perp ON\left(đpcm\right)\)

a: Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét ΔBAC có
BN là đường cao ứng với cạnh huyền AC
CM là đường cao ứng với cạnh huyền AB
BN cắt CM tại H
Do đó: AH⊥BC


1.Xét tứ giác CEHD ta có:
Góc CEH = 900 (Vì BE là đường cao)
Góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEC = 900.
CF là đường cao => CF ┴ AB => góc BFC = 900.
Như vậy E và F cùng nhìn BC dưới một góc 900 => E và F cùng nằm trên đường tròn đường kính BC.
Vậy bốn điểm B,C,E,F cùng nằm trên một đường tròn.
3. Xét hai tam giác AEH và ADC ta có: góc AEH = góc ADC = 900; góc A là góc chung
=> Δ AEH ˜ Δ ADC => AE/AD = AH/AC=> AE.AC = AH.AD.
* Xét hai tam giác BEC và ADC ta có: góc BEC = góc ADC = 900; góc C là góc chung
=> Δ BEC ˜ Δ ADC => AE/AD = BC/AC => AD.BC = BE.AC.
4. Ta có góc C1 = góc A1 (vì cùng phụ với góc ABC)
góc C2 = góc A1 ( vì là hai góc nội tiếp cùng chắn cung BM)
=> góc C1 = góc C2 => CB là tia phân giác của góc HCM; lại có CB ┴ HM => Δ CHM cân tại C
=> CB cũng là đương trung trực của HM vậy H và M đối xứng nhau qua BC.
5. Theo chứng minh trên bốn điểm B, C, E, F cùng nằm trên một đường tròn
=> góc C1 = góc E1 (vì là hai góc nội tiếp cùng chắn cung BF)
Cũng theo chứng minh trên CEHD là tứ giác nội tiếp
góc C1 = góc E2 (vì là hai góc nội tiếp cùng chắn cung HD)
góc E1 = góc E2 => EB là tia phân giác của góc FED.
Chứng minh tương tự ta cũng có FC là tia phân giác của góc DFE mà BE và CF cắt nhau tại H do đó H là tâm đường tròn nội tiếp tam giác DEF.

1. Xét tứ giác CEHD ta có:
góc CEH = 900 (Vì BE là đường cao)
góc CDH = 900 (Vì AD là đường cao)
=> góc CEH + góc CDH = 1800
Mà góc CEH và góc CDH là hai góc đối của tứ giác CEHD. Do đó CEHD là tứ giác nội tiếp
2. Theo giả thiết: BE là đường cao => BE ┴ AC => góc BEA = 900.
AD là đường cao => AD ┴ BC => BDA = 900.
Như vậy E và D cùng nhìn AB dưới một góc 900 => E và D cùng nằm trên đường tròn đường kính AB.
Vậy bốn điểm A, E, D, B cùng nằm trên một đường tròn.
3. Theo giả thiết tam giác ABC cân tại A có AD là đường cao nên cũng là đường trung tuyến
=> D là trung điểm của BC. Theo trên ta có góc BEC = 900.
Vậy tam giác BEC vuông tại E có ED là trung tuyến => DE = 1/2 BC.
4. Vì O là tâm đường tròn ngoại tiếp tam giác AHE nên O là trung điểm của AH => OA = OE => tam giác AOE cân tại O => góc E1 = góc A1 (1).
Theo trên DE = 1/2 BC => tam giác DBE cân tại D => góc E3 = góc B1 (2)
Mà góc B1 = góc A1 (vì cùng phụ với góc ACB) => góc E1 = góc E3 => góc E1 + góc E2 = góc E2 + góc E3
Mà góc E1 + góc E2 = góc BEA = 900 => góc E2 + góc E3 = 900 = góc OED => DE ┴ OE tại E.
Vậy DE là tiếp tuyến của đường tròn (O) tại E.
5. Theo giả thiết AH = 6 Cm => OH = OE = 3 cm.; DH = 2 Cm => OD = 5 cm. Áp dụng định lí Pitago cho tam giác OED vuông tại E ta có ED2 = OD2 – OE2 ↔ ED2 = 52 – 32 ↔ ED = 4cm

a: Xét (O) có
ΔBMC nội tiếp
BC là đường kính
Do đó: ΔBMC vuông tại M
=>CM\(\perp\)MB tại M
=>CM\(\perp\)AB tại M
Xét (O) có
ΔBNC nội tiếp
BC là đường kính
Do đó ΔBNC vuông tại N
=>BN\(\perp\)NC tại N
=>BN\(\perp\)AC tại N
Xét ΔABC có
BN,CM là các đường cao
BN cắt CM tại H
Do đó: H là trực tâm của ΔABC
b: Gọi K là giao điểm của AH và BC
Xét ΔABC có
H là trực tâm của ΔABC
K là giao điểm của AH và BC
Do đó: AH\(\perp\)BC tại K
Ta có: ΔAMH vuông tại M
mà ME là đường trung tuyến
nên EM=EH
=>ΔEMH cân tại E
=>\(\widehat{EMH}=\widehat{EHM}\)
mà \(\widehat{EHM}=\widehat{KHC}\)(hai góc đối đỉnh)
và \(\widehat{KHC}=\widehat{ABC}\left(=90^0-\widehat{MCB}\right)\)
nên \(\widehat{EMH}=\widehat{ABC}\)
Ta có: OM=OC
=>ΔOMC cân tại O
=>\(\widehat{OMC}=\widehat{OCM}\)
Ta có: \(\widehat{EMO}=\widehat{EMH}+\widehat{OMC}\)
\(=\widehat{ABC}+\widehat{OCM}\)
\(=90^0\)
=>ME là tiếp tuyến của (O)
c: Gọi I là giao điểm của EO và MN
Ta có: ΔHAN vuông tại N
mà NE là đường trung tuyến
nên NE=AE=ME
Ta có: NE=ME
=>E nằm trên trung trực của NM(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OE là đường trung trực của MN
=>OE\(\perp\)MN tại trung điểm I của MN
Xét ΔMEO vuông tại M có MI là đường cao
nên \(MI\cdot EO=ME\cdot MO\)
=>\(2\cdot MI\cdot EO=2\cdot ME\cdot MO\)
=>\(MN\cdot OE=2\cdot ME\cdot MO\)

a: góc OAC+góc OHC=180 độ
=>OACH nội tiếp
b: Xét ΔOKM vuông tại K và ΔOHC vuông tại H có
góc O chung
=>ΔOKM đồng dạng với ΔOHC
=>OK/OH=OM/OC
=>OK*OC=OH*OM