Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BHCK có
I là trung điểm của BC
I là trung điểm của HK
Do đó: BHCK là hình bình hành

a,
Ta có ON // BH ( cùng vuông góc với AC )
OM // AH ( cùng vuông góc với BC )
MN // AB ( MN là đường trung bình của tam giác ABC )
Vậy tam giác OMN đồng dạng với tam giác HAB.
b,
Xét tam giác AHG và MOG có :
\(+,\widehat{HAG}=\widehat{OMG}\)( Do AH // OM )
\(+,\frac{OM}{AH}=\frac{MN}{AB}=\frac{1}{2}=\frac{GM}{GA}\)( DO 2 TAM GIÁC ĐỒNG DẠNG Ở CÂU a, )
Từ đó ta có tam giác AHG đồng dạng với tam giác MOG(c.g.c) nên \(\frac{OG}{HG}=\frac{MG}{MA}=\frac{1}{2}\)
Và \(\widehat{HGO}=\widehat{HGA}+\widehat{AGO}=\widehat{OGM}+\widehat{AGO}=\widehat{AGM}=180^0\)
\(\Rightarrow H,G,O\)thẳng hàng

a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O
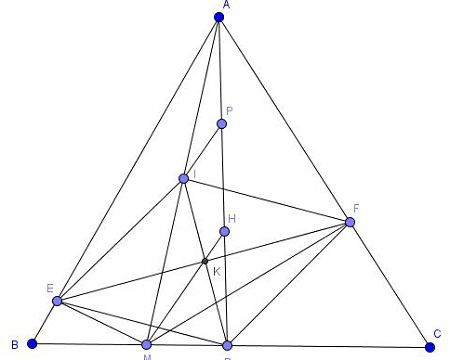
a) Các tam giác vuông AEM và ADM có EI và DI là trung tuyến ứng với AM nên
=> EI = DI ( = ½ AM)
=> Tam giác EID cân tại I
Lại có các tam giác AEI và ADI cân tại I nên:
^EIM = 2^EAI và ^MID = 2^IAD
=> ^EID = ^EIM + ^MID = 2(^EAI + ^IAD) = 2^EAD = 2. 30 = 60 độ
(Vì AD là đường cao nên là phan giác ^A)
Tam giác EID cân lại có ^EID = 60 độ nên đều
Tương tự tam giác IFD đều nên: EI = IF = FD = DE => Tứ giác DEIF là hình thoi
b) Gọi O là giao EF và DI và K là trung điểm AH, ta có IK là trng bình tam giác AMH và OH là trung bình tam giác AID.
=> HO//IK và HM//IK
=> Tia HO và HM trùng nhau hay M, H, O thẳng hàng => MH, ID, EF đồng quy tại O
a: O là giao điểm của 3 đường trung trực của ΔABC
=>O là tâm đường tròn ngoại tiếp ΔABC
=>AM là đường kính của (O)
Xét (O) có
ΔABM nội tiếp đường tròn
AM là đường kính
=>ΔABM vuông tại B
=>BM vuông góc AB
=>BM//CH
Xét (O) có
ΔACM nội tiếp
AM là đường kính
=>ΔAMC vuông tại C
=>AC vuông góc CM
=>CM//BH
Xét tứ giác BHCM có
BH//CM
BM//CH
=>BHCM là hình bình hành
=>BC cắt HM tại trung điểm của mỗi đường
=>I là trung điểm của HM
b: Xét ΔMAH có
O,I lần lượt là trung điểm của MA,MH
=>OI là đường trung bình
=>OI//AH và OI=1/2AH
=>AH=2OI