Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
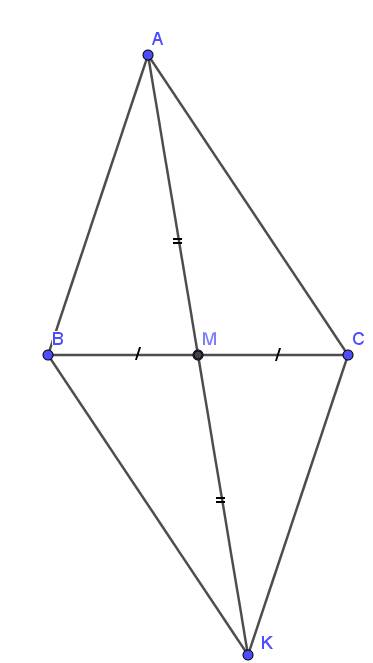
| GT | ΔABC cân tại A M là trung điểm của BC MK=MA MH\(\perp\)AB; MK\(\perp\)AC H\(\in\)AB; K\(\in\)AC |
| KL | b: ΔABM=ΔACM c: ΔABM=ΔKCM d: AB//CK e: MH=MK |
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
c: Xét ΔMAB và ΔMKC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMKC
d: Ta có: ΔMAB=ΔMKC
=>\(\widehat{MAB}=\widehat{MKC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//KC
e: ΔAMB=ΔAMC
=>\(\widehat{MAB}=\widehat{MAC}\)
Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
=>MH=MK
=>ΔMHK cân tại M

Giả sử tam giác ABC vuông tại A óc góc B = 60 độ
Để AI = IM thì I là trung điểm của AM
=> BI là trung tuyến cũng là đường cao
=> tam giác ABM cân tại B có góc B = 60 độ
=> tam giác ABM đều
Tương tự cho MK và KD.
Vậy khi tam giác ABC vuông tại A với AB < AC và góc B = 60 độ thì AI = IM = MK = KD.

Lời giải:
a. Xét tam giác $AMC$ và $KMB$ có:
$MC=MB$ (do $M$ là trung điểm $BC$)
$AM=KM$ (gt)
$\widehat{AMC}=\widehat{KMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle KMB$ (c.g.c)
và $\widehat{ACM}=\widehat{KBM}$
Mà 2 góc này ở vị trí so le trong nên $AC\parallel BK$
b.
Xét tam giác $ABM$ và $KCM$ có:
$BM=CM$
$AM=KM$
$\widehat{AMB}=\widehat{KMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle KCM$ (c.g.c)
$\Rightarrow \widehat{ABM}=\widehat{KCM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CK$

Vì \(\Delta AMB=\Delta AMC\) (cmt)
\(\Rightarrow\) góc BAM = góc CAM
Xét \(\Delta AHM\) và \(\Delta AKM\) có:
góc AHM = góc AKM = \(90^0\)(vì \(MH\perp AB;MK\perp AC\)) (gt)
AM chung
góc HAM = góc KAM (vì góc BAM = góc CAM)
\(\Rightarrow\Delta HAM=\Delta KAM\) (cạnh huyền - góc nhọn)
\(\Rightarrow MH=MK\) (2 cạnh tương ứng)
Lưu ý: từ "góc" trong bài là phải kí hiệu lên nhé; ở trong này mik ko biết kí hiệu mũ nên mik viết từ "góc" rồi ak. Mong bạn chú ý ak chứ viết vào vở có chữ "góc" là ko có điểm đâu nhé!