Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
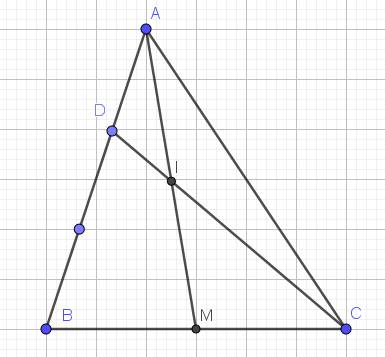
Áp dụng định lý Menelaus cho tam giác $ABM$ và $D,I,C$ thẳng hàng:
$\frac{AD}{DB}.\frac{IM}{IA}.\frac{CB}{CM}=1$
$\Rightarrow \frac{1}{2}.\frac{IM}{IA}.2=1$
$\Rightarrow \frac{IM}{IA}=1\Rightarrow IM=IA$ hay $I$ là trung điểm của $AM$.
Tiếp tục áp dụng định lý Menelaus cho tam giác $CBD$ có $I,A,M$ thẳng hàng:
$\frac{MC}{MB}.\frac{ID}{IC}.\frac{AB}{AD}=1$
$\Rightarrow 1.\frac{ID}{IC}.3=1$
$\Rightarrow \frac{ID}{IC}=\frac{1}{3}\Rightarrow CI=3DI$

a) Xét tam giác BDC có:
M là trung điểm BC(gt)
E là trung điểm DC(DE=EC)
=> ME là đường trung bình
=> ME//BD
b) Xét tam giác AME có:
ME//BD
D là trung điểm AE(AD=DE)
=> I là trung điểm AM
c) Xét tam giác AME có:
D là trung điểm AE(AD=DE)
I là trung điểm AM(cmt)
=> ID là đường trung bình
\(\Rightarrow ID=\dfrac{1}{2}ME\)
Mà \(ME=\dfrac{1}{2}BD\)(do ME là đường trung bình tam giác BDC)
\(\Rightarrow ID=\dfrac{1}{2}.\dfrac{1}{2}BD=\dfrac{1}{4}BD\)