Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối A với O.
Ta có: SABN = 1/3 SBNC nên đường cao kẻ từ A và C xuống NB có tỉ lệ 1/3
Suy ra SABO = 1/3 SBOC (chung đáy OB)
Tương tự:
SAMC = 1/2SBMC nên dường cao kẻ từ A và B xuống MC có tỉ lệ 1/2
Suy ra SAOC = 1/2 SBOC (chung đáy OC)
Từ đó ta có: SAOC + SAOB = (1/3+1/2)SBOC = 5/6 SBOC
SAOC + SAOB có 5 phần thì SBOC có 6 phần và SABC có (5+6) 11 phần
Vậy: AOCB = 6/11 SABC

Vì AN = NC nên NC = 1/2 AC
Vì AM = MB nên MB = 1/2 AB
S BNC = 1/2 S ABC ( Vì có chung h B ->AC và NC = 1/2 AC)
S BMC = 1/2 S ABC ( Vì có chung h C ->AB và MC = 1/2 AB)
=> S BMC = S BNC
Mà 2 tam giác này đều chứa chung S BIC nên S NIC = S BIM
Đ/s: S NIC = S BIM

đề này đúng ra nó phải cho thêm dữ kiện về AB,AC chứ bạn

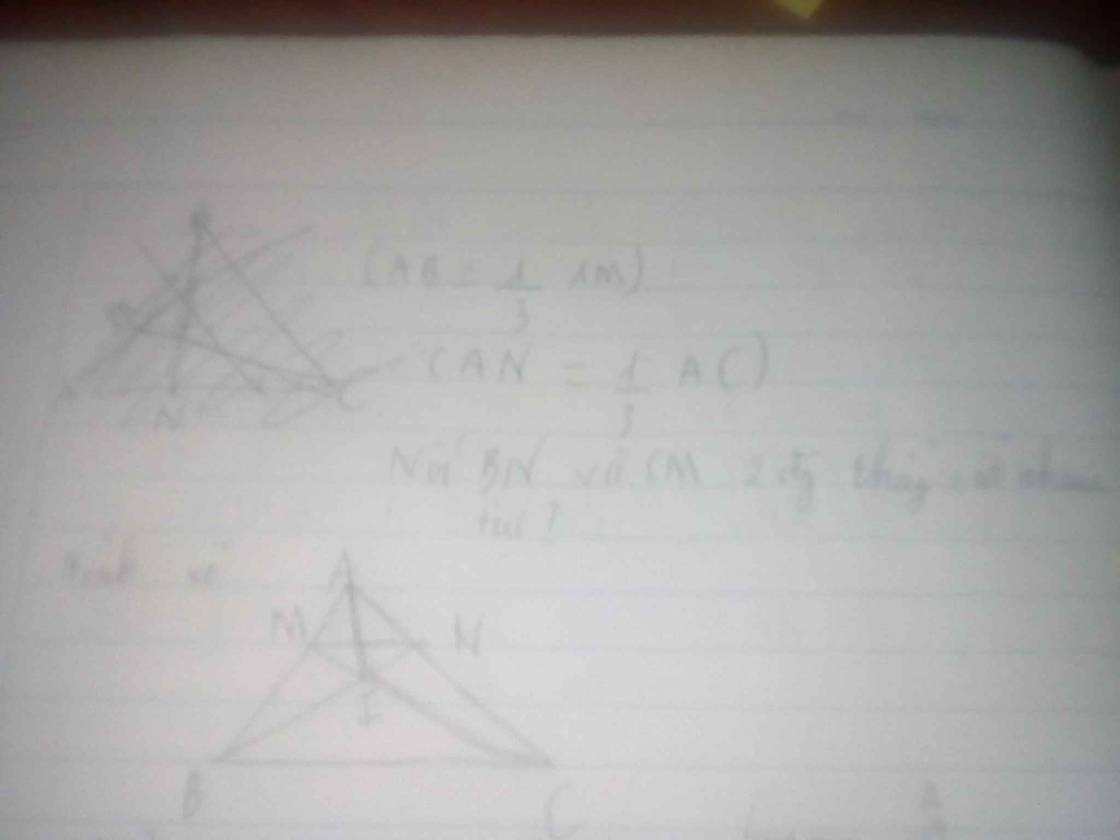 cái này là hình vẽ nhé!
cái này là hình vẽ nhé!
a, Tam giác AIB và tam giác ABC có chung chiều cao hạ từ B xuống AC, đáy AN = 1/3 đáy AC.
=> SAIB = 1/3 x S ABC.
Tam giác AIC và ABC có chiều cao hạ từ C xuống ABC, đáy AM = 1/3 đáy ABC.
=> SAIC = 1/3 x SABC.
=> SAIB = SAIC ( Vì cùng bằng = 1/3 SABC)
câu b thì bạn chưa nói rõ nên mình đưa bạn bản mẫu là tứ giác và 90cm2 nhé!
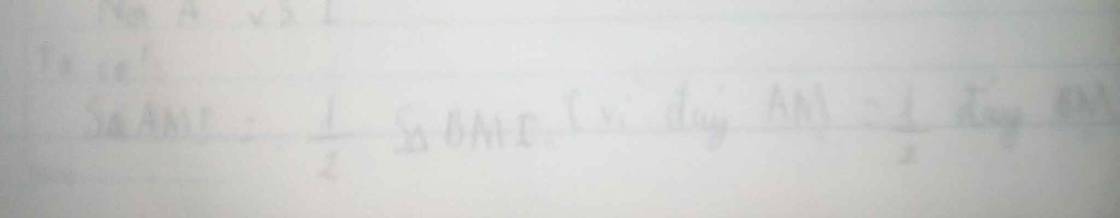 Ta có :
Ta có :
SAMI = 1/2 SƠMI ( vì đáy ÂM = 1/2 đáy BM)
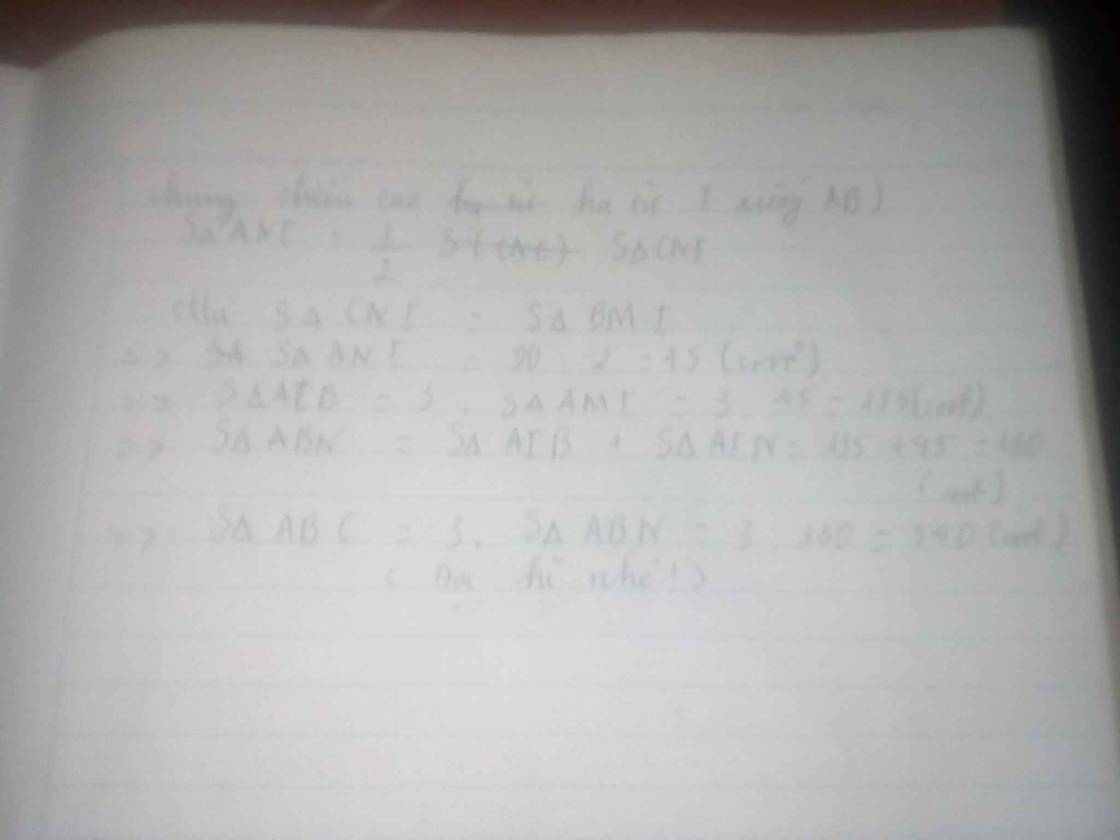 bạn thông cảm vì máy chụp hơi kém nhé!
bạn thông cảm vì máy chụp hơi kém nhé!