Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta thấy: DE song song với BC, N nằm trên DE => ND, NE đều song song với BC.
Áp dụng định lý Thales vào tam giác ABM và AMC, có NB và NC lần lượt song song với MB, MC nên:
\(\hept{\begin{cases}\frac{AN}{AM}=\frac{ND}{MB}\\\frac{AN}{AM}=\frac{NE}{MC}\end{cases}}\Leftrightarrow\frac{ND}{MB}=\frac{NE}{MC}\Leftrightarrow\frac{ND}{NE}=\frac{MB}{MC}\)
(đpcm)

Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của DB
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DC
Xét ΔAME có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
hay AI=IM

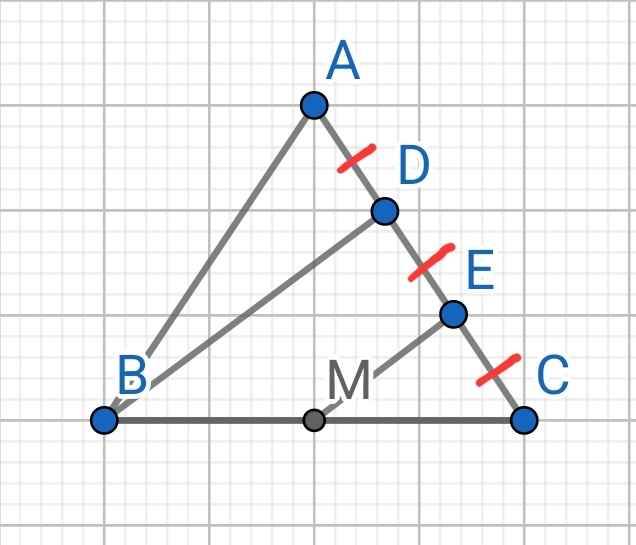
Sửa đề:
AD = DE = EC. BD cắt AM tại I
GIẢI
a) Sửa đề: Chứng mình BDEM là hình thang
Do DE = EC (gt)
⇒ E là trung điểm DC
Mà M là trung điểm BC (gt)
⇒ ME là đường trung bình của ∆BCD
⇒ ME // BD
Tứ giác BDEM có:
ME // BD (cmt)
⇒ BDEM là hình thang
b) Do AD = DE (gt)
⇒ D là trung điểm của AE
Do BD // ME (cmt)
⇒ BI // ME
Mà D là trung điểm của AE (cmt)
⇒ I là trung điểm của AM
⇒ IA = IM

vì DE // BC
=> DN // BM
VÀ EN // MC
=> DN/BM = EN/CM = AN/AM
=> DN = CN

Xét ΔAMB có ND//MB
nên ND/MB=AN/AM
Xét ΔAMC có NE//MC
nên NE/MC=AN/AM
=>ND/MB=NE/MC
=>ND=NE