Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn ơi xem lại đề đi nha , ko có đường tròn sao lại có đường kính AH

a: Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó: ΔABD vuông tại B
=>BD//CH
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>CD//BH
Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>I là trung điểm của HD
Xét ΔDAH có DI/DH=DO/DA
nen Io//AH và IO=AH/2
=>AH=2OI

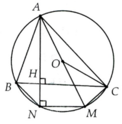
a, Ta có A C M ^ = 90 0 (góc nội tiếp)
b, Ta có ∆ABH:∆AMC(g.g)
=> B A H ^ = O A C ^ ; O C A ^ = O A C ^
=> B A H ^ = O C A ^
c, A N M ^ = 90 0
=> MNBC là hình thang
=> BC//MN => sđ B N ⏜ = sđ C M ⏜
=> C B N ^ = B C M ^ nên BCMN là hình thang cân

a: góc ACM=1/2*sđ cung AM=90 độ
b: góc ADB=góc AEB=90 độ
=>ABDE nội tiếp
^BAC = 90 ° (tg ABCv tại A)
^CDB = 90 ° (BH vg CE tại D)
=>Tứ giác ADBC nội tiếp
b)Xét tứ giác ADBC nội tiếp có
^ADH = ^ACB (góc ngoài = góc đối trong)
AB cắt CD tại E
=> khi E di động trên AB thì ^ADH 0 đổi
c)tgKBE ∽ tgABC (gg) =>KB/AB = BE/BC
=>KB.BC = BE.AB (1)
tgKCE ∽ tg DBC (gg) => KC/DC = CE/CB
=>KC.CB = CE.DC (2)
Từ (1) và (2) =>BE.AB=CE.DC
=> Khi E di động trên AB thì BE.AB + CE.DC không đổi
ủa bạn đề đâu có cho ABC vuông đâu ạ ?